Chama-se potência de uma lente, o inverso de sua distância focal (se for medida em , se mede em ). Considere duas lentes delgadas de potências e em contato uma com a outra. Mostre que equivalem a uma única lente de potência (soma algébrica).
Passo 1
Vamos considerar duas lentes delgadas em contato uma com a outra:
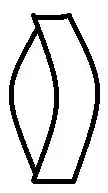
Para a primeira lente, temos que
Já para a segunda lente, o primeiro raio é (o mesmo que o segundo raio da primeira) e o segundo é :
Passo 2
Por outro lado, podemos encarar o sistema das duas lentes juntas como uma única lente com raios e . Assim, o foco resultante seria
Mas note que curioso:
Daí,
Portanto,
Passo 3
Mas como , e , segue que
Era isso que o exercício pediu para mostrarmos.
Resposta
Demonstração.