Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 28
Uma lente delgada biconvexa tem distância focal .
a) Demonstre que a distância mínima entre um objeto e sua imagem real é igual a . Para que distância do objeto à lente esse mínimo é atingido?
b) Qual é o aumento lateral na situação do mínimo?
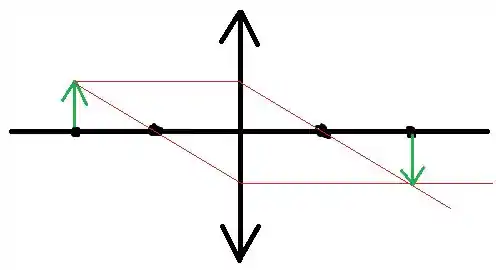
c) Desenhe o traçado de raios correspondentes à situação do mínimo, tomando como objeto uma seta perpendicular ao eixo.
Passo 1
Se a imagem é real, ela é formada atrás da lente com . Assim, a distância do objeto até a imagem será
Portanto,
Sabemos que
Substituindo :
Logo,
Com isso,
Ou ainda
Passo 2
Fazendo o mmc:
Logo,
Ou ainda,
Para que essa equação tenha solução real, devemos ter
Mas note que
Logo, para que , devemos ter
Desta forma, a condição é
Vemos que a distância mínima do objeto a sua imagem deve ser .
Passo 3
Usando , temos que
Logo,
Portanto, temos que
Passo 4
Para calcular o aumento lateral, usamos a fórmula
Como :
Portanto,
A representação dos raios que formam a imagem é dada a seguir:
