Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.1 - Ex. 4
Lesões à coluna vertebral. No tratamento de lesões da coluna, em geral é necessário fornecer uma tensão ao longo da coluna vertebral para esticá-la. Um dispositivo para fazer isso é a estrutura de Stryker (Figura ). Um peso é preso ao paciente (��s vezes, em torno de um colar cervical, Figura ), e o atrito entre o corpo da pessoa e a cama impede o deslizamento. (a) Se o coeficiente de atrito estático entre o corpo de um paciente de e a cama é , qual é a força de tração máxima ao longo da coluna vertebral que pode fornecer sem fazer com que o paciente deslize? (b) Sob as condições de tração máxima, qual é a tensão em cada cabo preso ao colar cervical?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a força de tração máxima ao longo da coluna vertebral e a tensão em cada cabo preso ao colar cervical.
Nós sabemos que o coeficiente de atrito estático entre o corpo e a cama é , para um paciente de massa . Então, para obter a tensão máxima, temos que considerar que o paciente está pronto para deslizar, assim, o atrito estático está no máximo e as forças sobre ele somam zero. Então, basta aplicarmos a segunda lei de Newton no sistema em equilíbrio () para obtermos a força desejada nos dois casos.
Vamos lá!
Passo 2
a) O diagrama de corpo livre para a pessoa é dado na figura (a):
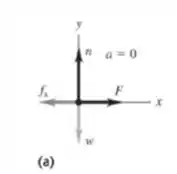
é a magnitude da tração ao longo da coluna vertebral e é o peso da pessoa. No atrito estático máximo, a força de atrito é .
Então, observando o diagrama da figura, temos:
E na horizontal:
Usando a fórmula da força de atrito:
E substituindo o valor do coeficiente de atrito:
Então, substituindo , com e , vamos ter:
Passo 3
b) O diagrama de corpo livre para o colar onde os cabos são fixados é dado na figura (b). A tensão
em cada cabo foi resolvido em seus componentes e .
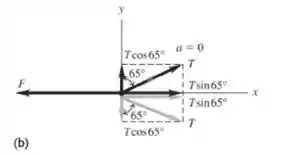
Observando o diagrama, temos:
Então, isolando na equação:
Para , vamos ter:
E considerando o peso , obtemos:
Valeu, galera! Até a próxima! 😉