Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 55
Um lingote de cobre de a é colocado em de água a em um recipiente isolado. (Os calores específicos estão na Tabela ).
Qual é a temperatura de equilíbrio do sistema cobre-água?
Que variação de entropia
o cobre,
a água e
o sistema cobre-água sofrem até atingirem a temperatura de equilíbrio?
Passo 1
(a)Olá pessoal, tudo bem? Vamos treinar um pouco de entropia e primeira lei? Bora lá?
A temperatura de equilíbrio do sistema é determinada somando todos os calores envolvidos no sistema e igualando tudo a zero. Ou seja, o equilíbrio ocorre quando:
Mas pra não ficar muito complicado, vamos por partes, ok? ;)
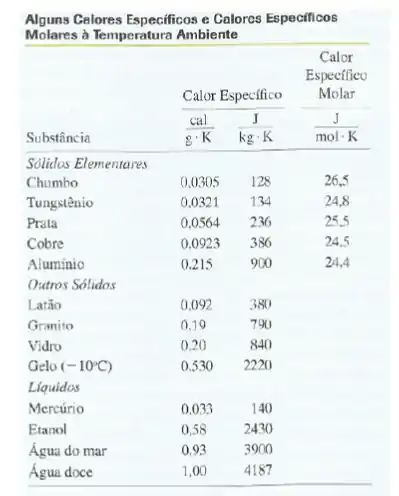
Aqui vou usar a massa em gramas e o calor específico em e a temperatura em ok?
- Para o cobre:
- Para a água:
Agora vamos somar os calores e igualar a zero:
Então essa é a temperatura de equilíbrio!
Passo 2
(b)A variação de entropia para cada parte do sistema vai ser dada pela fórmula:
E temos que:
Vamos fazer por partes?
Passo 3
Para o cobre, agora que temos a temperatura de equilíbrio, podemos calcular a variação de entropia. Te liga que o calor vai ser dado em calorias, e a variação de entropia é em . Pra transformar, é só multiplicar no final por , ok?
Dá uma espiada ali em cima no passo e pega a fórmula para :
Substituindo os valores:
Passo 4
(c)Para a água, com a temperatura de equilíbrio, podemos calcular a variação de entropia. Dá uma espiada de novo no passo , pega a fórmula, mas agora aplica pra água:
Substituindo os valores:
Passo 5
(d)A variação de entropia do sistema vai ser a soma das variações individuais: