Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 21
Uma linha de cargas com densidade linear uniforme está ao longo do eixo desde até , onde . Mostre que a componente do campo elétrico em um ponto no eixo é dado por , onde , e .
Passo 1
A figura abaixo ilustra o que o enunciado diz.
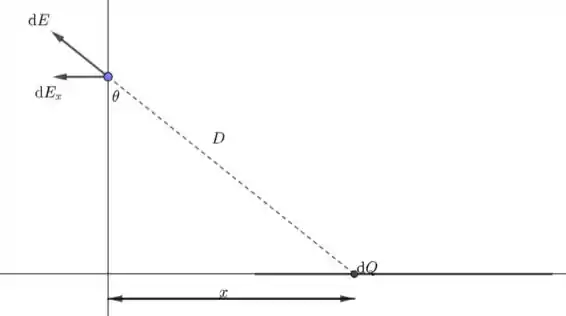
Notemos que
Assim, a componente será:
Como
segue que
Passo 2
A expressão do campo elétrico poderá ser escrita como
O campo elétrico total é obtido integrando-se de até . Sendo assim,
que é o que queríamos provar (note que acima calculamos o módulo; a expressão dada no enunciado leva em conta que )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Faça um gráfico quantitativo do campo elétrico ao longo do eixo central de um anel de diâmetro 6,0cm carregado uniformemente com uma carga total de 1,0 ∙ 10 8 C .
A que distancia ao longo do eixo central de um anel de raio R, carregado uniformemente, o modulo do campo elétrico é máximo?
Na Fig. 24-34, duas barras finas de plástico, uma de carga +q e a outra de carga −q, formam um círculo de raio R num plano xy. Um eixo x passa pelos pontos que unem as duas barras e a carga em cada um
Uma barra fina, não-condutora, de comprimento finito L, tem uma carga q uniformemente distribuída ao longo dela. Mostre que o módulo E do campo elétrico no ponto P sobre a mediatriz da barra é dado po