Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 26

Uma fina casca hemisférica de raio R tem uma densidade superficial uniforme de carga σ . Determine o campo elétrico no centro da base da casca hemisférica.

Passo 1

A figura a seguir ilustra o enunciado.

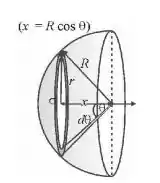
Vamos começar calculando o campo elétrico devido ao anel destacado na figura. Suponha que esse anel possua carga d Q . Note que, pela simetria, o campo irá apontar como indica a flechinha da figura. Assim,

d E = k   d Q R 2 cos ⁡ θ = k x R 3 d Q

Precisamos calcular d Q . Note que o anel possui largura R   d θ e comprimento 2 π r , sendo r = R sen ⁡ θ . Sendo assim, sua área será

d A = R   d θ 2 π r = 2 π R 2 sen ⁡ θ   d θ

Dessa forma, a carga no anel será:

d Q = σ d A = 2 π R 2 σ sen ⁡ θ   d θ

Ou seja, o campo elétrico será:

d E = k x R 3 2 π R 2   σ sen ⁡ θ   d θ = 2 π σ k x R sen ⁡ θ d θ

Como x = R cos ⁡ θ , segue que

d E = 2 π σ k cos ⁡ θ sen ⁡ θ d θ = π σ k sen ⁡ 2 θ   d θ

pois temos 2 sen ⁡ θ cos ⁡ θ = sen ⁡ 2 θ . Usando k = 1 / 4 π ε 0 , segue

d E = σ 4 ε 0 sen ⁡ 2 θ d θ

Passo 2

Obtemos o elemento de campo de cada anel! Vamos agora obter o campo resultante, fazendo o ângulo variar de 0 até π / 2 (pois dessa maneira a gente consegue percorrer todo o hemisfério). Assim,

E = σ 4 ε 0 ∫ 0 π / 2 sen ⁡ 2 θ d θ = σ 4 ε 0 - 1 2 cos ⁡ 2 θ 0 π / 2 E = σ 4 ε 0 - 1 2 - 1 - 1 = σ 4 ε 0

Resposta

O campo elétrico vale σ / 4 ε 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A resistência elétrica do ar é “rompida” quando a intensidade de campo elétrico atinge 3,0 ×10 6 N C , causando uma descarga. Um capacitor de placas paralelas é construído com dois discos de 4,0c m de
Um elétron é solto, em repouso, a 2,0 cm de um plano infinito carregado. Ele acelera em direção ao plano e colide com ele a uma velocidade de 1,0 ×10 7 m s . Quais são a densidade superficial de carga
Dois discos com 10 cm de diâmetro são colocados frente a frente e afastados por 20 cm. O disco da esquerda é carregado com - 50n C , e o da direita, com+ 50n C .Qual é o campo elétrico E → , em módulo
Dois anéis carregados, com 10 cm de diâmetro cada, são colocados frente a frente e afastados por 20 cm. O anel da esquerda está carregado com - 20n C , e o da direita, com + 20n C . Qual é o campo elé
Dois anéis com 10 cm de diâmetro estão carregados com + 20n C . Qual é a intensidade do campo elétrico no ponto eqüidistante aos dois anéis e;no centro do anel da esquerda?