Um anel de raio tem uma distribuição de cargas que varia como , como mostra a figura 22-39. (a) Quais são a direção e o sentido do campo elétrico no centro do anel? (b) Qual é a magnitude do campo no centro do anel?
Passo 1
- Notemos que . Como para , segue que a parte superior do anel está positivamente carregado, enquanto que a parte inferior está negativamente carregada. Inicialmente, vamos analisar a parte superior do anel. Como , segue que o campo elétrico devido a parte superior deve estar localizado verticalmente para baixo. Veja:
- Do que foi dito anteriormente, podemos simplesmente tomar o campo elétrico no eixo de cada quarto da circunferência e depois simplesmente multiplicar por . Veja:
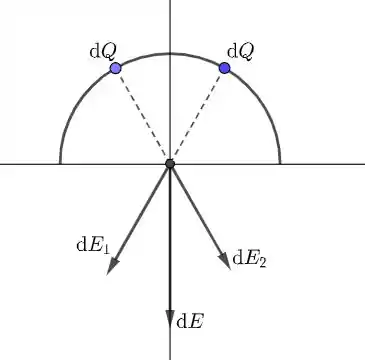
Argumento semelhante mostra que o campo elétrico devido a parte de baixo também estará orientado verticalmente para baixo. Dessa forma, temos que , com .
Passo 2
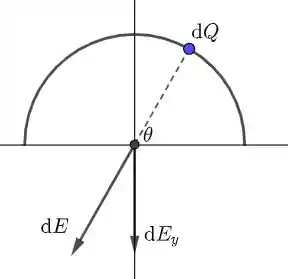
Temos que
Como
Segue que:
Agora,
Integrando de até , temos
Como
segue que
Passo 2
Assim, o campo elétrico total será:
Em termos vetoriais,
Resposta
- Vertical para baixo