Uma barra fina, não-condutora, de comprimento finito L, tem uma carga q uniformemente distribuída ao longo dela. Mostre que o módulo E do campo elétrico no ponto P sobre a mediatriz da barra é dado por:
Passo 1
Bora timeee, que o jogo com o Responde Aí fica fácil, então segue o jogo aqui que você vai fazer um golaço, pega aí um elemento infinitesimal da barra contém uma carga , na qual é a densidade linear de carga. Por simetria, as componentes horizontais dos campos produzidos pelos elementos de carga se cancelam e precisamos apenas calcular, por integração, a soma das componentes verticais. A simetria do problema também permite calcular apenas a contribuição de metade da barra e multiplicar o resultado por dois. No cálculo que se segue, fazemos uso do fato de que , na qual .
Passo 2
Agora família vamos iniciar os cálculos pega só, a partir da equação do campo elétrico para uma carga pontual:
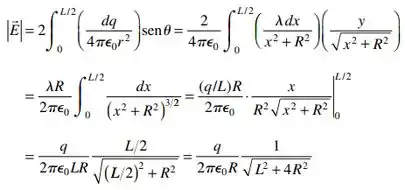
Resposta
Dessa forma podemos confirmar que: