Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 12
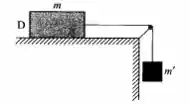
Em lugar de realizar a experiência da pg. 69 aplicando a força F através de um esforço muscular, podemos aplicá-la ao disco D de massa m através da força-peso de uma massa m’ suspensa da forma indicada na figura, ligada a D por um fio que passa sobre uma polia (supondo desprezíveis as massas do fio e da polia). a) Calcule a magnitude a da aceleração do disco e mostre que, se m’ é desprezível em confronto com m, a é diretamente proporcional a m´ e inversamente proporcional a m. b) Calcule a tensão T no fio ( força aplicada a D ) e mostre que, nas mesmas condições, ela se aproxima da força-peso.
Passo 1
- Bom pessoal, podemos fazer todo o diagrama de forças e analisar um sistema de equações, mas é melhor usar a famosa malandragem e juntar os 2 corpos como um sistema único onde as trações seriam forças internas que se cancelam!
- Como queremos a tração vamos analisar o corpo D, cuja força resultante é simplesmente a tração.
Nesse caso a força que é aplicada no sistema só depende da massa , então fica assim
Se estivermos considerando muito pequena em relação a , dividir por dá no mesmo que dividir por , belê? Então seria
( é diretamente proporcional a e inversamente proporcional a )
Passo 2
Se quisermos analisar o caso em que vamos modificar um pouco a fórmula.
Vamos aplicar isso na nossa fórmula de tração
Bom, como então de modo que podemos desprezar o termo na equação acima. Logo
Isso faz sentido já que se o corpo de cima for muiiiito pesado nosso sistema mal vai se mover (considera-se parado já que ).