Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 5
O sistema representado na figura está em equilíbrio. Determine as tensões nos fios 1, 2 e 3 e o valor do ângulo .
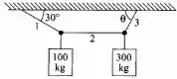
Passo 1
Nesse problema vamos analisar os nós, no nó da esquerda temos 3 forças atuantes, uma é a tração da corda que segura o peso de 100 kg e as outras são as trações .
- Nesse primeiro caso temos
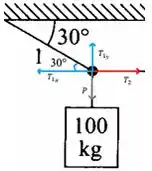
Passo 2
No nó da direita podemos montar uma equação similar já que se anulam vetorialmente, ficamos assim ó
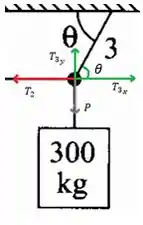
(dividindo a equação de baixo pela de cima)
Resposta
Exercícios de Livros Relacionados
O sistema da Fig. 12-75 está em equilíbrio. Os ângulos são θ 1 = 60 º º e θ 2 = 20 º º e a bola tem uma massa M=2,0 kg. Qual é a tensão (a) da corda ab e (b) da corda bc?
A Fig. 12-90 mostra um cilindro horizontal de 300 kg sustentado por três fios de aço presos em um teto. Os fios 1 e 3 estão nas extremidades do cilindro e o fio 2 está no centro. Os fios têm uma seção
A Fig.. 12-82 mostra um arranjo estacionário de duas caixas de lápis e três cordas. A caixa A tem uma massa de 11,0 kg e está sobre uma rampa de ângulo θ = 30,0 º º; a caixa B tem uma massa de 7,00 kg
Um sistema de cordas e polias é usado para erguer um corpo de massa M (Figura 12-52) com rapidez constante. Quando a extremidade da corda se desloca de uma distância L, para baixo, a altura da polia d
Uma placa de massa M, com a forma de um triângulo equilátero, está suspensa por um de seus vértices, e uma massa m está suspensa no outro vértice. Se a base do triângulo forma um ângulo de 6,0° cm a h