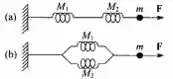
Na figura, as molas têm massa desprezível, o mesmo comprimento relaxado e constantes de mola ,respectivamente. Mostre que se pode substituir o par de molas por uma mola única equivalente de constante de mola k e calcule k nos casos a) e b).
Passo 1
- Nesse primeiro caso a força exercida em cada uma das molas tem o valor F e gera deslocamento diferentes já que as constantes são diferentes. Se quisermos o mesmo efeito (aceleração) gerado por outra mola equivalente é preciso que seu deslocamento seja de . Traduzindo isso pela lei de hooke temos
- Aqui podemos pensar que os deslocamentos são iguais já que as 2 molas estão conectadas no mesmo ponto do sistema. Além disso, as forças somadas que a mola faz para trás têm que ser iguais, somadas, as que uma única mola faria.