Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 5
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:
Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.
Identifique o “sistema” em seu diagrama de interação.
Desenhe um diagrama de corpo livre para cada objeto do sistema. Use linhas tracejadas para conectar os membros de um mesmo par ação/reação.
|| O bloco da FIé mais pesado do que o bloco B e está escorregando para baixo em uma rampa. Todas as superfícies têm atrito. A corda é desprovida de massa, e as polias são todas desprovidas de massa e giram sobre esferas livre de atrito. A corda e a polia estão entre os objetos que interagem, mas você terá de decidir se elas fazem ou não parte do sistema.
Passo 1
Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.
No diagrama de interação, representamos as forças que atuam no sistema, e lembrando que há diferentes tipos de força, nesse caso podemos esquematizar assim:
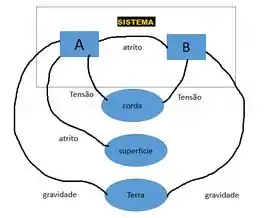
Passo 2
Identifique o “sistema” em seu diagrama de interação.
O “sistema” consiste nos dois blocos e , são eles que interagem com o meio, no nosso esquema eles estão dentro do retângulo.
Passo 3
Desenhe um diagrama de corpo livre para cada objeto do sistema. Use linhas tracejadas para conectar os membros de um mesmo par ação/reação.
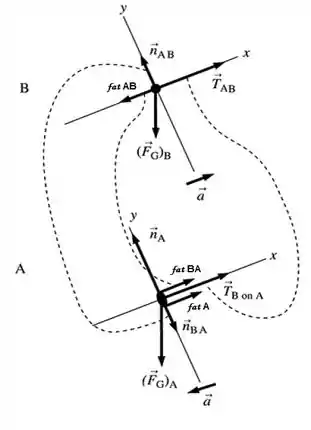
Desenhando as forças, observando que é plano inclinado, ficamos com:
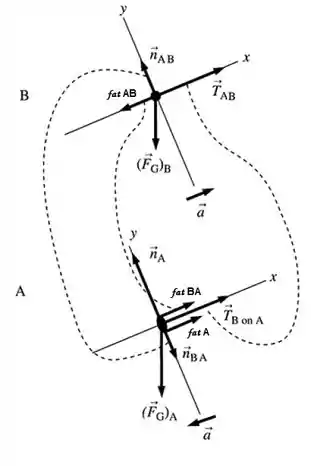
As tensões, tem que serem iguais para que o sistema se mantenha em equilíbrio, lembrando que a normal, não forma par de ação e reação com a força peso(), e que a aceleração vai se anular tb.
Resposta
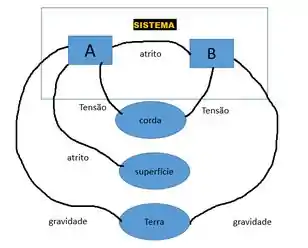
O “sistema” consiste nos dois blocos e , são eles que interagem com o meio, no nosso esquema eles estão dentro do retângulo.
