Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 39
Luz branca incide em um ângulo de com a normal a um plano que tem um par de fendas separadas por . Quais comprimentos de onda na região do visível dão máximos de interferência na luz transmitida na direção normal ao plano? (Veja o Problema 38.)
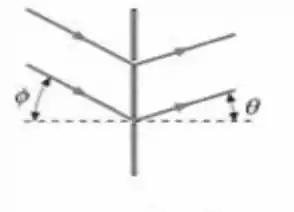
Passo 1
Meus amigos e minhas amigas!
Para encontrar os comprimentos de onda na região do visível que dão máximos de interferência na luz transmitida, podemos proceder da seguinte forma:
Relacionar as duas equações:
Passo 2
Vamos dar início:
Vamos igualar as equações:
Vamos considerar :
Vamos aplicar os valores fornecidos:
Analisando a tabela:
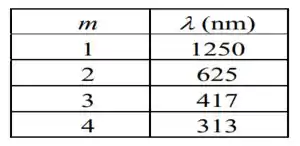
Constatamos que 625 nm e 417 nm são comprimentos de onda na região do visível que fornecem máximos de interferência na luz.
Resposta
625 nm e 417 nm
Exercícios de Livros Relacionados
No experimento de Young, com a luz incidindo perpendicularmente sobre o anteparo onde estão os dois orifícios, coloca-se uma lâmina delgada transparente de faces paralelas e índice de refração n sobre
Um padrao de interferincia de fenda duplaeformado usando luz de laser monocromatica com comprimento de onda de 450 nm. Oque acontece com a distancia entre o primeiro maximo e o maximo central quando a
Um experimento de interferencia de fenda dupla e montado em uma camara na qual e possivel fazer vacuo.Usando luz de um laser de helio-neonio,um padrdo de interterencia e observado quando a camara esta
Um padrao de interferencia de fenda duplaeformado usando luz de laser monocromatica com comprimento de onda de 640 nm.No primeiro minimo do maximo central,qual ea diferenca de caminho optico entre a l
A Equacao 33-2,que e d sen 0=mA,e a Equacao 33-11, que easen 0=mA,algumas vezes sao confundidas.Para cada equacao.defina os simbolos e explique a aplicacao de cada equacao.