Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 11
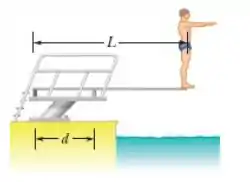
Um mergulhador com de peso está em pé na extremidade de um trampolim de comprimento e massa desprezível. O trampolim está preso em dois suportes separados por uma distância . Das forças que agem sobre o trampolim, qual é (a) o módulo e (b) o sentido (para cima ou para baixo) da força exercida pelo suporte de trás e (c) o módulo e (d) o sentido (para cima ou para baixo) da força exercida pelo suporte da frente? (e) Que pedestal (o de trás ou da frente) está sendo tracionado e (f)que pedestal está sendo comprimido?
Passo 1
(a)Belezera galerinha bonita, primeiro vamos tomar a força vertical do suporte da esquerda como sendo igual a . Além disso, considere a força que o suporte da direita exerce sobre o trampolim. Essas forças, bem como a força que o mergulhador exerce sobre o trampolim (que é igual ao peso do mergulhador) estão representados na figura:
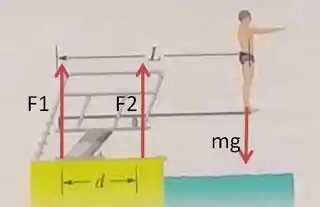
Do equilíbrio na vertical, obtemos a relação:
Além disso, o equilíbrio de torques, com relação ao eixo que passa pelo suporte da direita, nos leva à seguinte expressão:
Logo:
Subsituindo os valores que conhecemos:
Ou em :
Passo 2
(b)Como o sinal de que encontramos acima é negativo, podemos afirmar que ela está direcionada para baixo.
Passo 3
(c)Agora, podemos encontrar por meio da expressão que já apareceu acima (). Como já temos o valor de , podemos substituir o valor dela nessa expressão para encontrar :
Logo:
Ou em :
Passo 4
(d)Como encontrada acima é positiva, temos que ela está direcionada para cima, assim como a nossa hipótese inicial.
Passo 5
(e)Como a força que o suporte exerce sobre o suporte da esquerda é para baixo, pela lei de ação e reação, a força que o trampolim exerce sobre o suporte da esquerda está no sentido contrário, para cima. Logo, esse suporte está sendo tracionado (o mesmo que “esticado”).
Passo 6
(f)Como encontrada é positiva (direcionada para cima), a força que o trampolim exerce sobre o suporte da direita está para baixo (pela lei de ação e reação). Então, esse suporte está sendo comprimido.
Resposta
(a)
(b)Para baixo
(c)
(d)Para cima