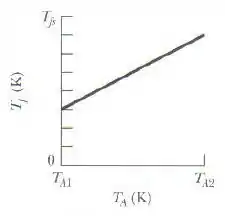
Em uma série de experimentos, um bloco é colocado em um recipiente termicamente isolado em contato com um bloco , que tem a mesma massa que o bloco . Em cada experimento, o bloco está inicialmente à temperatura , mas a temperatura do bloco varia de experimento para experimento. Suponha que representa a temperatura final dos dois blocos ao atingirem o equilíbrio térmico. A figura mostra a temperatura em função da temperatura inicial para um intervalo de valores de , de até . Qual é (a) a temperatura e (b) a razão entre os calores específicos dos blocos?

Agora vamos tentar fazer o seguinte: achar aquela função que está representada no gráfico! Como ela mostra a temperatura final dos corpos em função da temperatura inicial , vamos tentar isolar a .

Tá, vamos “abrir" esses parênteses:

Beleza, achamos uma boa expressão. Lembra que o gráfico é em função de ? Como ele é uma reta, isso quer dizer o seguinte:

E quem vai ser o coeficiente angular da reta?

E o coeficiente linear é:

Nessa edição do livro, o enunciado não diz qual é a escala do eixo , mas não dá pra resolver sem saber ela. Em outras edições, a gente encontra , então vamos usar isso.

O coeficiente angular é a inclinação da reta, certo?

Se a escala do eixo é , então cada um dos oito “traços” ali vale , e então:

Beleza, e o coeficiente linear vai ser simplemente o ponto onde a reta cruza o eixo :

(a) Ok, agora sim, vamos resolver aquele sistema ali de cima:

Primeiro vamos usar o sistema pra achar . Isolando ele na segunda equação:

E como a gente faz pra misturar a primeira equação nessa aí? Bom, primeiro é interessante perceber que a fração nessa última equação parece um pouco com o inverso da primeira lá de cima, né? A única diferença é o ao invés do , mas isso a gente corrige:

Beleza? Pode ser meio estranho, mas essa é uma substituição muito usada na física quando você quer trocar o numerador em uma fração desse tipo:

Enfim, voltando lá na equação que a gente estava fazendo:

Pronto! Foi difícil, mas foi.

(b) Agora a questão é encontrar a razão entre os dois calores específicos. Sem problemas, vamos voltar no nosso sistema, agora com o valor de :

Vamos ajeitar um pouco essa segunda equação:

Então o sistema fica assim:

Ótimo, agora é só dividir a segunda equação pela primeira:

Cortando os denominadores (já que são iguais):

Resolvido!