Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 4
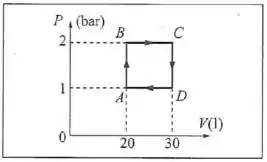
Um mol de um gás ieal diatômico () descreve o ciclo , onde é medido em e em . (a) Calcule a temperatura nos vértices. (b) Calcule a eficiência de um motor térmico operando segundo esse ciclo. (c) Compare o resultado (b) com a eficiência máxima ideal associada às temperaturas extremas do ciclo.
Passo 1
(a) Vamos calcular a temperatura em cada um dos vértices utilizando a lei dos gases ideais:
Então, sabendo que e :
Passo 2
(b) Agora vamos calcular a variação da energia interna em cada uma das etapas. Para isso precisamos calcular :
Substituindo a segunda equação na primeira:
E o enunciado já deu , então:
Agora podemos calcular :
Passo 3
E para poder calcular o calor trocado em cada etapa, também precisamos calcular o trabalho realizado em cada trecho.
Em e o trabalho é nulo, porque os processos são isovolumétricos. E os outros dois são isobáricos:
Então o trabalho total realizado pelo gás é:
E agora podemos calcular o calor absorvido pelo gás em cada etapa usando a primeira lei da termodinâmica:
Quando temos , isso indica que o gás está absorvendo calor. São esses valores que precisamos considerar no cálculo da eficiência, então:
Passo 4
(c) Agora vamos calcular a eficiência máxima permitida nessa situação.
No nosso caso, a temperatura da fonte fria é e a temperatura da fonte quente é :
Resposta
(a) , , , .
(b) .
(c) .