Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 5
Um gás ideal com sofre uma expansão isotérmica em que seu volume aumenta de , seguida de uma contração isobárica até o volume inicial e de aquecimento, a volume constante, até a temperatura inicial. (a) Calcule o rendimento deste ciclo. (b) Compare o resultado com o rendimento de um ciclo de Carnot que opere entre as mesmas temperaturas externas.
Passo 1
Vamos começar fazendo um diagrama do processo descrito no enunciado:
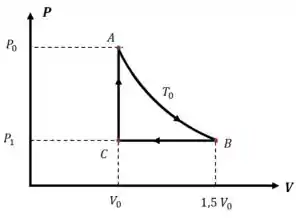
Para calcular o rendimento desse ciclo, precisamos calcular o trabalho total e o calor absorvido pelo gás:
E para encontrar essas duas grandezas, precisamos determinar a temperatura e a pressão .
Começamos comparando os pontos e , que têm a mesma temperatura:
E como e :
E podemos comparar os pontos e , que têm o mesmo volume, para encontrar a temperatura :
E como , e , temos:
Agora vamos substituir isso tudo no gráfico:
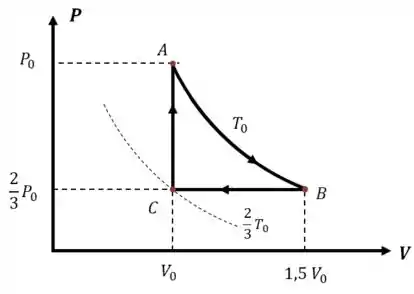
Passo 2
Agora sim, podemos calcular o trabalho realizado nesse processo.
Vamos tentar escrever tudo em função de e . Começando pelo processo , que é isotérmico:
No processo , que é isobárico, temos:
E pela lei dos gases ideais temos :
E no processo , que é isovolumétrico, temos .
Então o trabalho em um ciclo completo é:
Passo 3
Agora vamos calcular o calor total fornecido para o gás.
No trecho , que é isotérmico, temos:
Então, pela primeira lei da termodinâmica:
No trecho , o gás está indo para uma temperatura mais baixa, portanto nenhum calor é fornecido para ele.
No trecho , podemos calcular o calor através da variação de energia interna, já que :
E então o calor total é:
Agora podemos calcular a eficiência:
Passo 4
(b) Agora queremos calcular qual seria o rendimento de um ciclo de Carnot que operasse entre essas duas temperaturas.
Nosso reservatório frio está a temperatura , e o reservatório quente está a . Então o rendimento de um ciclo de Carnot seria:
Resposta
(a) .
(b) .