Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 17

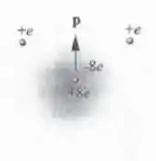
A molécula de água, , possui uma configuração de cargas que pode ser representada qualitativamente como na Figura 16.9. Os dois átomos de perdem seus elétrons para o átomo de , de forma que este fica com uma carga líquida , enquanto cada átomo de fica reduzido a um próton com carga . Para distâncias bastante maiores que o diâmetro da molécula, o campo elétrico gerado pela mesma equivale ao de um dipolo elétrico. Os dois prótons são substituídos por uma carga situada no ponto médio entre os prótons da Figura 16.8, e toda a carga do íon é posicionada sobre a mediatriz da linha que liga os dois prótons. O valor medido do dipolo é . Calcule (A) a distância entre o centro das cargas positivas e o centro das cargas negativas ; (B) o campo elétrico no ponto da Figura 16.8 acima do centro da molécula .

Passo 1

Eae galera! Belezinha? Vamos lá! A carga do dipolo que a questão nos dá é de:

Sabemos que a formula do dipolo é dada por:

Logo,

Passo 2

Para acharmos o campo elétrico, vamos calcular a partir da formula padrão usando a carga do dipolo.

Sendo o centro da molécula. Logo,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O elipsóide metálico mostrado na figura 16.12 possui carga líquida + q . Esboce qualitativamente a distribuição das cargas no corpo e as linhas de força do campo elétrico.

A Figura 16.13 mostra uma agulha de tungstênio, cuja ponta tem um raio de curvatura de 0,01μ m , próxima de uma placa condutora. Entre a placa e a agulha existe uma diferença de potencial de 10V . (A)

Duas cascas esféricas condutoras concêntricas de raios R 1 e R 2 estão carregadas com cargas de sinais opostos e módulo q , como se vê na figura 16.7. Calcule a energia associada ao campo elétrico ger

Quatro cargas de módulo q , duas positivas e duas negativas, estão situadas nos vértices de um quadrado de lado L . As cargas de mesmo sinal ocupam os vértices opostos do quadrado. Calcule a energia p