Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 5
Quatro cargas de módulo , duas positivas e duas negativas, estão situadas nos vértices de um quadrado de lado . As cargas de mesmo sinal ocupam os vértices opostos do quadrado. Calcule a energia potencial eletrostática do sistema.
Passo 1
Eae galera! Belezinha? Então, nessa questão vamos primeiro entender duas cositas. A primeira, é a fórmula da energia potencial eletrostática entre duas cargas. Ela é dada por:
A segunda coisa pra gente entender nessa questão, é como vamos organizar as formulas. Temos que a energia potencial eletrostática do sistema, é dada pela soma de cada energia potencial entre duas cargas. Logo,
Isso, tomado a partir desse esquemático:
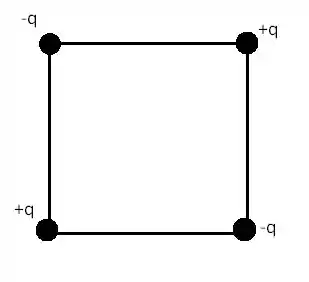
Passo 2
Agora, deixamos de enrolação e aplicaremos a formula!
Somando tudo, temos:
Resposta
Resposta
Exercícios de Livros Relacionados
Duas esferas metálicas de raios R e r , respectivamente, estão separadas por uma distância d muito maior do que R e r . Inicialmente, a esfera de raio R possui uma carga Q e a outra esfera está descar
Um cabo elétrico retilíneo infinito com seção circular de raio a tem uma densidade linear de carga uniforme igual a λ . Calcule a energia eletrostática por unidade de comprimento do cabo. Discuta o re
Calcule a densidade de energia do campo elétrico associado a uma placa infinita possuindo densidade uniforme de carga σ = 10,0μ C / m 2 .
Um dipolo elétrico está à distância r de uma carga + q , alinhado na orientação radial, como mostra a Figura 16.11. Calcule a força exercida sobre o dipolo.
Calcule o valor do potencial elétrico à distância d de um plano infinito com densidade σ uniforme de carga, tomando o ponto de referência no infinito.