Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 4.Problemas - Ex. 1b

Um motorista dirige para o sul a 20,0   m / s por 3,00   m i n , então vira para oeste e move-se a 25,0   m / s por 2,00   m i n , quando finalmente vai para o noroeste a 30,0   m / s por 1,00   m i n . Para esse percurso de 6,00   m i n , encontre (a) o vetor deslocamento total, (b) a velocidade escalar média e (c) a velocidade média. Considere o eixo positivo x como apontado para leste.

Passo 1

Eai Pessoal. Tudo bem?? Bora matar mais uma questão. Se liga nas dicas.

Vamos iniciar fazendo a representação dos vetores.

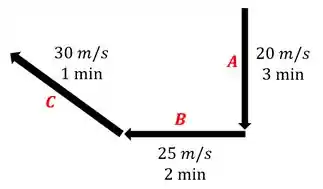
Agora vamos coloca-los em um sistema de coordenadas. Como vocês podem ver o último trajeto está na direção noroeste, ou seja, faz um ângulo de 45° com a horizontal.

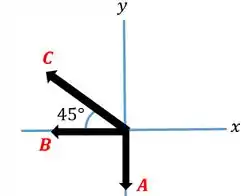
Mão a obra!

Passo 2

  1. Na letra a temos que calcular o deslocamento total. Vamos então usar a equação da velocidade média para descobrir o descolamento de cada trajeto e depois teremos que fazer o somatório em cada eixo.

    2. Deslocamento em A

    v = 20   m / s   e ∆ t = 180   s

    ∆ s = v . ∆ t

    ∆ s = 20.180

    ∆ s = 3600   m

    Deslocamento B

    v = 25   m / s   e ∆ t = 120   s

    ∆ s = v . ∆ t

    ∆ s = 25.120

    ∆ s = 3000   m

    Deslocamento C

    v = 30   m / s   e ∆ t = 60   s

    ∆ s = v . ∆ t

    ∆ s = 30.60

    ∆ s = 1800   m

    Vamos agora calcular o deslocamento total.

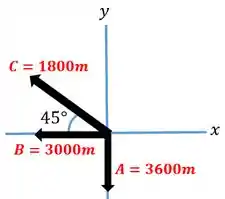
    Vamos iniciar com a decomposição do vetor C .

    V e t o r   C

    S x = S cos ⁡ 45 ° = 1800 . 2 2 = 900 2 = 1273   m

    S y = S sen ⁡ 45 = 1800 . 2 2 = 900 2 = 1273   m

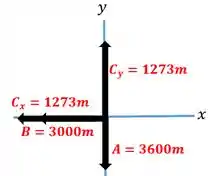
    Fazendo o somatório nos eixos. Temos.

    ∑ S x = 1273 + 3000 = 4273 m

    ∑ S y = 1273 - 3600 = 2327 m

    Aplicando o Teorema de Pitágoras.

    S 2 = 4273 2 + ( 2327 ) ²

    S = 4865   m

    Passo 3

  2. Para a velocidade, mas calcular a velocidade resultante.

    3. Vamos iniciar com a decomposição do vetor C .

    V e t o r   C

    v x = v cos ⁡ 45 ° = 30 . 2 2 = 15 2 = 21,2 m

    v y = v sen ⁡ 45 = 30 . 2 2 = 15 2 = 21,2   m

    Fazendo o somatório nos eixos. Temos.

    ∑ v x = 21,2 + 25 = 46,2   m / s

    ∑ v y = 21,2 - 20 = 1,2   m / s

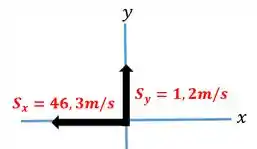
    Aplicando o Teorema de Pitágoras.

    v 2 = 46,3 2 + ( 1,2 ) ²

    v = 46,3   m / s

    Passo 4

  3. Para a velocidade média, temos.

v = ∆ S ∆ t

v = 4865 360 = 13,5   m / s

Resposta

  1. S = 4865   m
  2. 46 m/s
  3. 13,5 m/s

Exercícios de Livros Relacionados

Você deixa cair uma bola de futebol da janela do terceiro andar de uma loja. Usando as imagens de um filme, desenhe um diagrama de movimento básico, começando no instante que a bola é solta e terminan
Encontre o vetor aceleração média no ponto 1 do diagrama de movimento com três pontos mostrado na Figura EX1.9.A rapidez média do objeto entre os pontos 1 e 2 é maior, menor ou igual à rapidez média e
Uma jogadora de softball rebate a bola e começa a correr para a primeira base. Usando um modelo de partícula, desenhe um diagrama de movimento que mostre a posição da jogadora e seus vetores velocidad
Encontre o vetor aceleração média no ponto 1 do diagrama de movimento com três pontos mostrados na Figura EX1.10.A rapidez média do objeto entre os pontos 1 e 2 é maior, menor ou igual à sua rapidez m
Uma criança desliza com seu trenó sobre um trecho nivelado e suave de neve. Ela, então, encontra um trecho rochoso, onde escorrega até parar. Desenhe um diagrama de movimento completo da criança e seu