Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 63
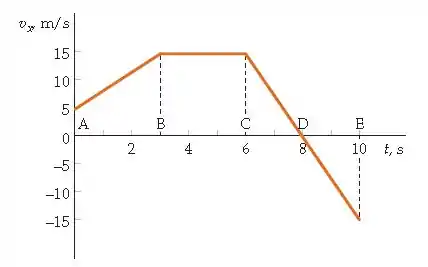
O movimento unidimensional de uma partícula está plotada na Figura 2-40. (a) Qual é a aceleração média em cada um dos intervalos AB, BC e CE? (b) A que distância a partícula está de seu ponto de partida após 10 s? (c) Esboce o deslocamento da partícula como função do tempo; assinale os instantes A, B, C, D e E em seu gráfico. (d) Quando é que a partícula está se deslocando o mais vagarosamente?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Nós podemos usar a definição de aceleração média , para encontrar a aceleração nos três intervalos solicitados.
Analisando o gráfico, para o intervalo AB, temos que a velocidade final é de 15 m/s e a velocidade inicial é de 5 m/s no intervalo de tempo de 3 segundos. Então:
Para o intervalo BC, temos que a velocidade final é de 15 m/s e a velocidade inicial é de 15 m/s no intervalo de tempo de 3 segundos. Então:
Para o intervalo CE, temos que a velocidade final é de -15 m/s e a velocidade inicial é de 15 m/s no intervalo de tempo de 4 segundos. Então:
Passo 2
Para encontrar a distância percorrida, devemos analisar cada parte do gráfico separadamente. Temos que:
Temos que , então:
Passo 3
Para esboçar o gráfico do deslocamento, precisamos encontrar a função que rege o movimento. Temos que:
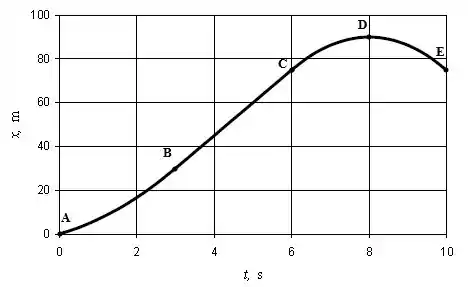
Para cada intervalo temos uma aceleração, então eles devem ser analisados separadamente. O seguinte gráfico pode ser gerado:
Passo 4
Para saber quando a partícula está se deslocando mais vagarosamente, é só analisar o gráfico do enunciado.
Temos que, no ponto D, quando , o gráfico cruza o eixo do tempo, onde a velocidade .