Em um CD, a música é codificada em uma configuração de minúsculos sulcos dispostos ao longo de uma trilha que avança formando uma espiral do interior à periferia do disco. À medida que o disco gira no interior de um aparelho de CD, a trilha é varrida com velocidade linear constante . Como o raio da trilha espiral aumenta à medida que o disco gira, a velocidade angular do disco deve variar enquanto o CD está girando. (Veja o Exercício .) Vejamos qual é a aceleração angular necessária para manter constante. A equação de uma espiral é dada por , onde é o raio da espiral para e é uma constante. Em um CD, é o raio interno da trilha espiral. Considerando o sentido da rotação do CD como positivo, deve ser positivo, de modo que e crescem à medida que o disco gira. (a) Quando o disco gira através de um pequeno ângulo , a distância varrida ao longo da trilha é . Usando a expressão anterior para , integre para calcular a distância total varrida ao longo da trilha em função do ângulo total u descrito pela rotação do disco. (b) Como a trilha é varrida com velocidade linear constante , a distância total encontrada na parte (a) é igual a . Use esse resultado para achar em função do tempo. Existem duas soluções para ; escolha a positiva e explique por que devemos escolhê-la. (c) Use sua expressão de para determinar a velocidade angular e a aceleração angular em função do tempo. O valor de é constante? (d) Em um CD, o raio da trilha mais interna é igual a , o raio da trilha cresce em cada volta e o tempo de duração é igual a . Calcule os valores de e de e ache o número total de voltas feitas durante o tempo total da reprodução do som. (e) Usando os resultados obtidos nos itens (c) e (d), faça um gráfico de (em rad/s) versus e um gráfico de (em rad/s2) versus até .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a distância total varrida ao longo da trilha em função do ângulo total, usar esse resultado para achar em função do tempo, determinar a velocidade angular e a aceleração angular em função do tempo, calcular os valores e de e esboçar um gráfico da velocidade e da aceleração angular em função do tempo, usando os dados obtidos.
Então, vamos lá!
Passo 2
- Calculando a distância total, vamos ter:
Onde deverá estar em radianos.
Passo 3
b) Temos
E uma solução positiva será
A solução negativa seria voltar para valores de menores do que .
Passo 4
c) Derivando a equação obtida no passo anterior, temos a velocidade angular:
E derivando mais uma vez, obtemos a aceleração angular:
Portanto, aceleração angular não é constante.
Passo 5
d) Para , deverá ser em radianos, então:
Usando da parte b, o ângulo total girado em é:
Passo 6
e) Os gráficos estão esboçados abaixo:
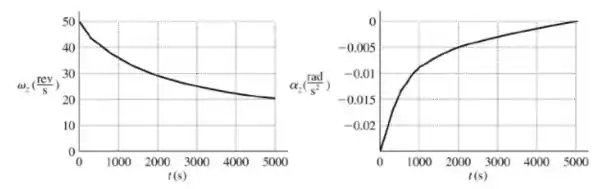
Valeu, galera! Até a próxima! 😉