Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 9.Problemas - Ex. 90

Determine o momento de inércia de um cone maciço uniforme em relação a um eixo que passa através de seu centro (Figura P 9.90 ). O cone possui massa M e altura h . O raio do círculo de sua base é igual a R .

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar o momento de inércia de um cone maciço uniforme em relação a um eixo que passa atrav��s de seu centro, segundo a figura:

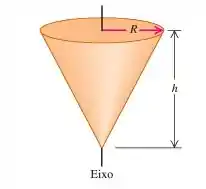
Nós sabemos que o cone possui massa M e altura h e que o raio do círculo de sua base é igual a R . Então, vamos aplicar a equação do momento de inércia:

I = ∫ r 2 d m

Seja z a coordenada do eixo vertical, vamos usar as seguintes fórmulas:

r z = z R h

d m = π ρ R 2 z 2 h 2  

d I = π ρ 2 R 4 h 4 z 4 d z

Vamos lá!

Passo 2

Considerando o momento de inércia:

I = ∫ d I

E substituindo a fórmula de d I vista no passo 1 :

I = π ρ 2 R 4 h 4 ∫ 0 h   z 4 d z

Então, integrando em relação a z , vamos ter:

I = π p 10 R 4 h 4 z 5 0 h

I = 1 10 π ρ R 4 h

O volume do cone é V = 1 3 π R 2 h , a massa é 1 3 π p R 2 h e então:

I = 3 10 π ρ R 2 h 3 R 2

I = 3 10 M R 2

Para um cilindro uniforme de raio R e para um eixo através de seu centro, I = 1 2 M R 2 . Para o cone é menos, como esperado, uma vez que o cone é construído a partir de uma série de discos paralelos cujos raios diminuem de R a zero ao longo do eixo vertical do cone.

Valeu, galera! Até a próxima! 😉

Resposta

3 10 M R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda de vagão de 1,00 m de diâmetro consiste em um aro fino de 8,00 k g de massa e de 6 raios, cada um com 1,20 k g de massa. Determine o momento de inércia da roda de vagão em relação ao seu eixo
Uma placa retangular uniforme tem massa m e lados de comprimentos a e b . (a) Mostre, por integração, que o momento de inércia da placa em relação a um eixo perpendicular passando por um dos vértices
Visando participar de uma equipe de atletas, você e seu amigo Carlos resolver praticar com halteres. Cada um de vocês está usando “A Besta”, um modelo constituído de duas esferas, cada uma de 500 g e
Ao tapear a superfície da água com sua cauda para anunciar perigo, um castor deve girá-la em torno de uma de suas extremidades estreitas. Modelemos a cauda como um retângulo de espessura e massa espec
Use integração para mostrar que o momento de inércia de uma casca esférica fina de raio R e massa m , em relação a um eixo que passa pelo seu centro, vale 2 m R 2 3 .