Uma nadadora visa diretamente a margem oposta de um rio, viajando a 1,6 m/s em relação à agua. Ela chega do outro lado 40 m rio abaixo. O rio tem uma largura de 80 m. (a) Qual é a rapidez da correnteza? (b) Qual é a rapidez da nadadora em relação a margem? (c) Em que sentido a nadadora deve apontar, se quiser chegar do outro lado do rio em um ponto diretamente oposto ao ponto de partida?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A imagem abaixo vai nos ajudar a entender melhor a situação:
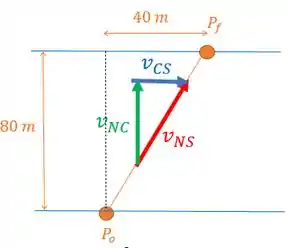
A nadadora mira um ponto na margem diretamente oposto ao seu ponto de partida. Isso quer dizer que a velocidade dela em relação a água é totalmente vertical porque ela quer andar uma trajetória vertical.
Só que há uma correnteza com velocidade em relação ao solo , paralela a margem do rio, que a faz andar em uma trajetória inclinada. Por isso ela chega 40 metros rio abaixo. Queremos saber o valor da velocidade da correnteza que proporcionou esta situação.
A velocidade dita a trajetória, por isso o vetor velocidade da nadadora em relação ao solo , que é a soma vetorial das outra duas velcoidades, vai ter a mesma orientação que sua trajetória.
Agora que a gente analisou o que está acontecendo, vamos para os itens!
Passo 2
a) Queremos o módulo de velocidade da nadadora em relação ao solo .
Como o tempo para sair de e chegar a é o mesmo tanto se a gente olhar o deslocamento vertical quando o horizontal da nadadora, podemos escrever:
E para achar o tempo decorrido de um percurso com velocidade constante, podemos usar:
Para o deslocamento vertical, temos:
Isso porque a correnteza dada por causa esse deslocamento horizontal. Já para o vertical:
Porque a distância percorrida é a largura do rio e a velocidade responsável por esse deslocamento é a velocidade imprimida pela nadadora na água . Igualando as duas expressões:
Passo 3
b) A rapidez da nadadora em relação à margem é o módulo de . A gente pode acha-lo usando trigonometria na nossa figura do passo 1. Fica assim:
Passo 4
c) Ele quer a orientação da velocidade da nadadora em relação a água para que ela faça a trajetória vertical, ou seja, para que seja vertical.
Lembrando que as velocidades envolvidas são ditadas pelas soma vetorial:
Então vamos desenhar essa soma, mas colocando como o vetor vertical e mantendo (velocidade da correnteza) paralela à margem do rio:

Queremos achar . Conhecemos o valor de porque essa velocidade depende da nadadora, e porque essa velocidade depende só da correnteza. Não sabemos porque aqui temos uma situação diferente da do item anterior, então o resultado da soma vetorial é diferente.
A gente pode usar trigonometria e escrever em função dos valores que a gente conhece. Assim:
Isolando quem a gente quer e substituindo nossos dados:
A nadadora deve se direcionar a 30° a esquerda da vertical para chegar na outra margem diretamente oposta ao ponto de saída.
Resposta
A nadadora deve se direcionar a 30° a esquerda da vertical para chegar na outra margem diretamente oposta ao ponto de saída.