Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 52

Uma partícula tem uma aceleração constante a → = 6,0 m s 2 i ^ + 4,0 m s 2 j ^ . No tempo t=0, a velocidade é zero e o vetor posição é r → 0 = 10   m i ^ . (a) Encontre os vetores velocidade e posição em função do tempo t. (b) Encontre a equação da trajetória da partícula no plano xy e esboce a trajetória.    

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A velocidade como função do tempo é dada por::

v → = v → 0 + a → t

Como a velocidade inicial é zero, temos:

v → = a → t

v → = 6,0 m s 2 i ^ + 4,0 m s 2 j ^ ⋅ t

A posição como função do tempo é dada por:

r → = r → 0 + v → 0 t + 1 2 a → t 2

Substituindo os valores, temos:

r → = 10   m i ^ + 1 2 6,0 m s 2 i ^ + 4,0 m s 2 j ^ t 2

Passo 2

A função horária, é obtida pela equação da posição para aceleração constante:

∆ S = v 0 t + 1 2 a t 2

Aplicando ao nosso problema nas coordenadas x e y, temos:

x = 10 + 3 t 2

y = 2 t 2

Isolando t 2 , e substituindo, temos:

y 2 = x - 10 3

y = 2 3 x - 20 3

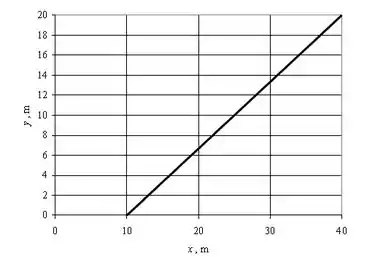
O gráfico para esta função é:

Resposta

a ) v → = 6,0 m s 2 i ^ + 4,0 m s 2 j ^ ⋅ t

r → = 10   m i ^ + 1 2 6,0 m s 2 i ^ + 4,0 m s 2 j ^ t 2

b ) y = 2 3 x - 20 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7 . || Um disco voador manobrando com aceleração constante é observado com as posições e velocidades mostradas naF I G U R AE X 4.7 . Qual é a aceleração a → do disco voador?
6 . || A trajetória de uma partícula é descrita por x = ( 1 2 t 3 - 2 t 2 ) m e y = ( 1 2 t 2 - 2 t ) m , onde t está em s . a. Quais são os valores da posição e da velocidade da partícula em t =0s e
8 . || Um disco de hóquei movido a foguete move-se sobre uma mesa horizontal sem atrito. A F I G U R AE X 4.8 mostra os gráficos de v x e de v y , os componentes x e y da velocidade do disco. Ele part
9 . || Um disco de hóquei movido a foguete move-se sobre uma mesa horizontal sem atrito. A F I G U R AE X 4.9 mostra os gráficos de v x e de v y , os componentesx ey da velocidade do disco. Ele parte
Uma partícula inicialmente localizada na origem tem aceleração de a →=3,00j ^m / s 2 e velocidade inicial de v i →=5,00i ^m / s . Encontre (a) o vetor posição da partícula em qualquer momento t , (b)