Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 54

Neste problema, 1,00 mol de um gás diluído tem, inicialmente, uma pressão de 1 , 00   a t m , um volume de 25L e uma energia interna de 456 J. Enquanto o gás é aquecido lentamente, a representação de seus estados em um diagrama PV move-se em linha reta até seu estado final. O gás tem, no final, uma pressão de 3,00 atm, um volume de 75L e uma energia interna de 912 J. Determine o trabalho realizado pelo gás e o calor por ele absorvido.

Passo 1

Fala! Então, ele quer o trabalho realizado pelo gás e o calor absorvido por ele. Como ele descreve o diagrama PV, é uma boa a gente esboçar ele.

Aqui, o processo consiste em um passo único, aonde o gás vai do ponto V 1 = 25   L e P 1 = 1   a t m até o ponto onde P 2 = 3   a t m   e V 2 = 75   L , em linha reta.

Lançando no diagrama:

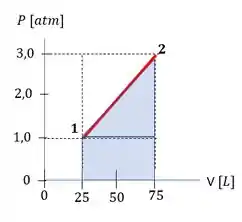
Aí ele pede o trabalho. Segundo a Primeira Lei da Termodinâmica, o trabalho realizado pelo gás pode ser calculado como a área abaixo do gráfico PV. Então o que a gente precisa fazer é calcular essa área azul. E com esse trabalho, conseguimos chegar no calor absorvido.

Bora lá!

Passo 2

A área azul é formada por uma figura geométrica conhecida, o trapézio. Então o trabalho do gás será:

W r e a l i z a d o   p e l o   g á s = A t r a p é z i o   = 1 2 B m e n o r   + B m a i o r   .   A l t u r a

Vamos definir cada um dos valores e transformar a pressão em Pa e o volume em m ³ .

Vamos lá?

B m e n o r   = 1   a t m × 101325   P a 1   a t m = 101325   P a

B m a i o r   = 3   a t m ×   101325   P a 1   a t m = 303976   P a

A l t u r a = 75 - 25 = 50   L

Vamos passar essa altura para m 3 :

A l t u r a = 75 - 25 L × 10 - 3   m 3 1 L = 0,05   m ³

Aqui a altura está com essa unidade porque ela não é uma altura real no espaço, é só a altura do trapézio do gráfico PV. Como o eixo horizontal está na unidade de volume, nossa altura do trapézio que é paralela a ele também vai estar em unidade de volume.

Jogando esses valores na expressão do trabalho:

W r e a l i z a d o   p e l o   g á s = 1 2 B m e n o r   + B m a i o r   .   A l t u r a

W r e a l i z a d o   p e l o   g á s = 1 2 101325 + 303976   0,0 5 = 10,1   k J

Finalizamos uma parte, mas ainda não acabou! Precisamos do calor absorvido.

Passo 3

Para determinar o calor absorvido precisamos lembrar do enunciado da primeira lei:

∆ E i n t = Q a b s o r v i d o + W s o b r e   o   g á s

Aqui entra um conceito bem importante, nós temos na fórmula o trabalho realizado sobre o gás, e só sabemos o valor do trabalho que o gás realiza, ou seja, o trabalho realizado pelo gás.

E como eles se relacionam? Fácil!

W s o b r e   o   g á s = - W r e a l i z a d o   p e l o   g á s

Substituindo na primeira lei:

∆ E i n t = Q a b s o r v i d o - W r e a l i z a d o   p e l o   g á s

Isolando o calor:

Q a b s o r v i d o = ∆ E i n t + W r e a l i z a d o   p e l o   g á s

Já temos o trabalho realizado pelo gás, do passo 2. Só precisamos da variação da energia interna. Como a gente faz? Cara, o enunciado nos deu a energia no início e no final, aí conseguimos calcular a variação:

∆ E i n t = E i n t . 2 - E i n t . 1 = 912   J - 456 J = 456   J

Jogando tudo na nossa expressão para o calor absorvido pelo gás:

Q a b s o r v i d o = ∆ E i n t + W r e a l i z a d o   p e l o   g á s

Q a b s o r v i d o = 456   J + 10,1   k J = 10,6   k J

Resposta

W r e a l i z a d o   p e l o   g á s = 10,1   k J ;

Q a b s o r v i d o = 10,6   k J .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque de aço contém 300g de amônia ( N H 3 ) a uma pressão de 1,35.10 6P a e uma temperatura de 77 ° C . (a) Qual é o volume do tanque em litros? (b) Mais tarde, a temperatura é 22 ° C e a pressão
Em certo processo, o calor liberado pelo sistema é 2,15 × 10 5J e, ao mesmo tempo, o sistema se contrai sob a ação de uma pressão externa constante igual a 9,50 × 10 5P a . A energia interna é a mesma
Três moles de gas argônio (considerado um gas ideal) originalmente a uma pressão de 1,50 × 10 4P a e a um volume de 0,0280m 3 são aquecidos e expandidos sob pressão constante até um volume de 0,0435m
Um volume de ar (considerado um gás ideal) é primeiro resfriado sem variação de volume, e depois expandido sem variação de pressão, como mostra o caminho a b c na Figura 19.30. a) Compare a temperatur
Durante certas estações, ventos fortes chamados de chinooks sopram do oeste e atingem o lesta das Montanhas Rochosas, descendo as montanhas até Denver e áreas adjacentes. Embora as montanhas sejam ria