Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 51

Nos Problemas 50 a 53, o estado inicial de 1,00 mol de um gás diluído é P 1 = 3,00   a t m ,   V 1 = 1,00   L   e   E i n t . 1 = 456   J ,   e seu estado final é P 2 = 2 , 00   a t m ,   V 2 = 3 , 00   L   e   E i n t . 2 = 912   J .

O gás é, primeiramente, resfriado a volume constante até atingir sua pressão final. Depois, ele se expande à pressão constante até atingir seu volume final.

  1. Ilustre este processo em um diagrama PV e calcule o trabalho realizado pelo gás;
  2. Determine o calor absorvido pelo gás durante este processo.

Passo 1

Bom, na letra a devemos fazer um diagrama Pressão x Volume. No primeiro processo o gás vai de P 1 = 3,00   a t m até P 2 = 2,00   a t m mantendo seu volume constante, V 1 = 1,00   L . Em seguida, mantendo sua pressão constante, se expande até V 2 = 3,00   L .

Lançando no diagrama:

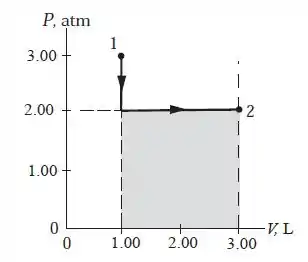
Ainda não acabou, certo? Precisamos do trabalho. Segundo a Primeira Lei da Termodinâmica, o trabalho pode ser calculado como:

W p e l o   g á s = P . ∆ V

Ou a área abaixo do gráfico, lembram?

Muito bem, no primeiro processo ∆ V = 0 , ou seja não temos trabalho. Antes de calcular o trabalho precisamos transformar a pressão em Pa e o volume em m³.

Vamos lá?

P = 2   a t m   x 101325   P a 1   a t m = 202650   P a

∆ V = 3 L - 1 L = 2 L   x 10 - 3 m 3 1   L = 2 x 10 - 3 m 3

Jogando no trabalho:

W p e l o   g á s = 202650   P a   x   2 x 10 - 3 m 3 = 405   J

Finalizamos a letra a e agora podemos passar para b.

Passo 2

Para determinar o calor absorvido precisamos lembrar do enunciado da primeira lei:

∆ E i n t = Q e n t r a + W s o b r e   o   g á s

Aqui entra um conceito bem importante, nós temos na fórmula o trabalho realizado sobre o gás, mas só sabemos o valor do trabalho que o gás realiza.

E como eles se relacionam? Fácil !

W s o b r e   o   g á s = - W p e l o   g á s

Substituindo:

∆ E i n t = Q e n t r a - W p e l o   g á s

Isolando o calor:

Q e n t r a = ∆ E i n t + W p e l o   g á s

Já temos o trabalho realizado pelo gás, do passo 1. Só precisamos da variação da energia interna:

∆ E i n t = E i n t . 2 - E i n t . 1 = 912   J - 456 J = 456   J

Jogando tudo na fórmula do calor:

Q e n t r a = 456   J + 405   J = 861   J

Resposta

  1. W p e l o   g á s = 405   J ;
  2. Q e n t r a = 861   J .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um mol de gás hélio, com C V = 3 2 R , inicialmente a 10a t m e 0 ° C , sofre uma expansão adiabática reversível até atingir a pressão atmosférica, como primeiro estágio num processo de liquefação do
No método de Rüchhardt para medir γ = C p / C V do ar, usa-se um grande frasco com um gargalo cilíndrico estreito de raio a , aberto para a atmosfera ( p 0 = pressão atmosférica), no qual se ajusta um
Um mol de um gás ideal, com C V = 3 2 R , a 17 ° C , tem sua pressão reduzida à metade por um dos quatro processos seguintes: (i) a volume constante; (ii) isotermicamente; (iii) adiabaticamente; (iv)
1g de gás hélio, com C V = 3 2 R , inicialmente nas condições N T P , é submetida aos seguintes processos: (i) Expansão isotérmica até o dobro do volume inicial; (ii) Aquecimento a volume constante, a
Um recipiente de paredes adiabáticas é munido de um pistão adiabático móvel, de massa desprezível e 200c m 2 de área,, sobre o qual está colocado um peso de 10k g . A pressão externa é de 1a t m . O r