Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 121

O oásis A está 90   k m a oeste do oásis B . Um camelo parte de A e leva 50   h para caminhar 75   k m na direção 37 ° ao norte do leste. Em seguida, leva 35   h para caminhar 65   k m para o sul e descansa por 5,0   h . Quais são (a) o módulo e (b) o sentido do deslocamento do camelo em relação a A até o ponto em que para para descansar? Do instante em que o camelo parte do ponto A até o final do período de descanso, quais são (c) o módulo e (d) o sentido da velocidade média do camelo e (e) a velocidade escalar média do camelo? A última vez que o camelo bebeu água foi em A ; o animal deve chegar a B não mais do que 120   h após a partida para beber água novamente . Para que chegue a B no último momento, quais devem ser (f) o módulo e (g) o sentido da velocidade média após o período de descanso?

Passo 1

Então galera , este problema lida com um movimento em duas dimensões de um camelo do oásis A para o oásis B . Bora dar uma olhada na figura a seguir para entendermos melhor o que está acontecendo . Usamos um sistema de coordenadas “convencional”, com o semieixo   x positivo apontando para leste e o semieixo y positivo apontando para o norte. As distâncias estão em quilômetros e os tempos em horas. Usando a notação vetorial, os primeiros dois deslocamentos da viagem são :

∆ r → 1 = 75 k m cos ⁡ 37 °   i → + 75 k m sen ⁡ 37 °   j →

∆ r → 2 = - 65 k m j →

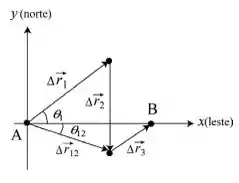
O deslocamento total é ∆ r → 12 = ∆ r → 1 + ∆ r → 2 . Como mostra a figura, para chegar ao oásis B é necessário um deslocamento adicional ∆ r → 3 .

Passo 2

Nós sabemos que o deslocamento total do camelo pode ser obtido através da relação :

∆ r → 12 = ∆ r → 1 + ∆ r → 2 = 60   k m i → - 20 k m j →

O módulo correspondente é ∆ r → 12 = 60 2 + - 20 2 = 63   k m

Passo 3

Usando a trigonometria básica , temos que a orientação de ∆ r → 12   pode ser obtida através da relação :

θ = tan - 1 ⁡ - 20 k m 63 k m = - 18 °

Ou seja , ∆ r → 12 está orientado a 18 ° ao sul do leste.

Passo 4

Para calcular a velocidade média nas duas primeiras partes do percurso usamos o resultado do item (a) na equação que já conhecemos , juntamente com o fato de que :

∆ t 12 = ∆ t 1 + ∆ t 2 + ∆ t d e s c a n s o = 50   h + 35 h + 5 h = 90   h

Na notação dos termos unitários , temos que :

v → 12 m é d = 60 i → - 20 j → k m 90   h = 0,67 i → - 0,22 j → k m h

Isso nos dá que :

v → 12 m é d = 0,67 2 + - 0,22 2 = 0,7   k m / h

Passo 5

Usando a trigonometria básica , temos que a orientação de v → 12 m é d   pode ser obtida através da relação :

θ = tan - 1 ⁡ - 0,22 0,67 = - 18 °

Ou seja , v → 12 m é d está orientado a 18 ° ao sul do leste.

Passo 6

A diferença entre a velocidade média e a velocidade escalar média é que a primeira depende do deslocamento total, enquanto a segunda depende da distância total percorrida. Como o camelo percorreu 140   k m , a velocidade escalar é :

( 140   k m ) / ( 90   h )   =   1,56   k m / h   ≈   1,6   k m / h .

Passo 7

O deslocamento total de A até B deve ser de 90   k m para leste. Vamos chamar de ∆ r → 3 o deslocamento do ponto onde o camelo parou para descansar até B . Nesse caso,

∆ r → 1 + ∆ r → 2 + ∆ r → 3 = 90 k m i →

o que nos dá ∆ r → 3 = 30   k m i → + 20   k m j →   na notação dos vetores unitários, ou ( 36   ∠   33 ° )na notação módulo-ângulo. Assim, de acordo com a equação da velocidade média, temos:

v → 3 m é d = 36 k m 120 - 90 h   = 1,2   k m / h

Passo 8

A orientação de v → 3 m é d é a mesma de ∆ r → 3 ( 33 ° ao norte do leste).

Tranquilo pessoal? Bora resolver mais questões então!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O vetor posição de um próton é inicialmente r →=5,0 i →- 6,0 j →+ 2,0 k → e depois se torna r → =- 2,0 i →+6,0 j →+ 2,0 k → , com todos os valores em metros. (a) Qual é o vetor deslocamento do próton?
A Fig. 4-61 mostra a trajetória seguida por um gambá bêbado em um terreno plano, de um ponto inicial i até um ponto final f Os ângulos são θ 1 =30,0 ° , θ 2 =50,0 ° e θ 3=80,0 ° ; as distâncias são d
Você foi sequestrado por estudantes de ciência política (que estão aborrecidos porque você declarou que ciência política não é ciência de verdade). Embora esteja vendado, você pode estimar a velocidad
Na Fig. 4-49, uma estação de radar detecta um avião que se aproxima, vindo do Leste. Quando é observado pela primeira vez, o avião está a uma distância d 1 = 360m da estação e θ 1 = 40 ° acima do hori
A velocidade de uma partícula é dada por v x = 7,0 m s 3 t 2 - 5,0 m s . Se a partícula está na origem em t 0 = 0 , encontre a função x ( t ) da posição.