Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 90
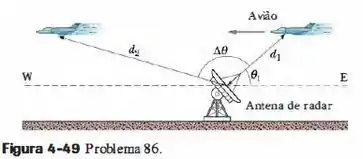
Na Fig. 4-49, uma estação de radar detecta um avião que se aproxima, vindo do Leste. Quando é observado pela primeira vez, o avião está a uma distância da estação e acima do horizonte. O avião é rastreado durante uma variação angular no plano vertical Leste-Oeste; a distância no final desta variação é . Determine (a) o módulo e (b) a orientação do deslocamento do avião durante este período.
Passo 1
Galera, vamos adotar o sentido positivo de para direita, o sentido positivo de para cima e a origem centrada na antena.
Agora precisamos encontrar a posição do avião no instante e no instante , lembrando que a coordenada e a coordenada .
(1) Ele faz um ângulo de e está a uma distância de , então suas coordenadas são:
(2) Ele faz um ângulo de e está a uma distância de , então suas coordenadas são:
Passo 2
O vetor deslocamento é dado pela diferença entre o vetor posição final e o vetor posição inicial.
Passo 3
Pessoal, o vetor deslocamento faz com o eixo um ângulo de .
Resposta
a)
b)