Um objeto está a à frente de uma lente convergente que tem distância focal igual a . Uma lente divergente que tem distância focal de magnitude igual a está localizada a atrás da primeira. (a) Determine a posição da imagem final e descreva suas propriedades (por exemplo, real e invertida) e (b) desenhe um diagrama de raios para corroborar suas respostas para a Parte (a).

Para a parte (a), começaremos pelo expressando a localização da primeira imagem pela equação (1) e depois aplicar os valores determinados na questão:

Ou seja, nenhuma imagem é formada na primeira lente; Com , a equação das lentes delgadas para a segunda lente se torna:

Determinada a distância da segunda imagem, agora iremos calcular a ampliação total do sistema de duas lentes, que equivale a ampliação da segunda lente:

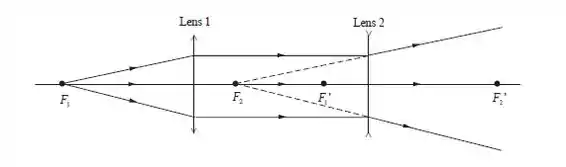
Com esses resultados, determinamos que a imagem final se encontra à do objeto, ela é virtual, direita e do mesmo tamanho que o objeto. Agora iremos para a parte (b).

Na parte (b) veremos que o diagrama de raios condiz com os resultados que encontramos anteriormente, observe:

PRONTO, fica bem, até a próxima!