Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Questões Conceituais - Ex. 15
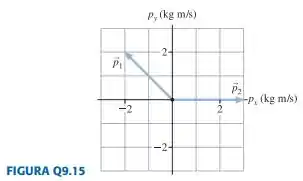
Um objeto em repouso explode e divide-se em três fragmentos. A FIGURA Q9.15 mostra os vetores momentum de dois fragmentos. Quais são e do terceiro fragmento?
Passo 1
Considerando que o objeto partiu da origem do sistema de coordenadas, e que partiu do repouso, vamos conservar o momentum total dos três fragmentos que ele se partiu.
Bom, se estava em repouso, o momentum total dos fragmentos precisa valer zero.
E, aqui, como estamos trabalhando com o sistema de coordenadas, temos que conservar o momentum tanto no eixo quanto no eixo .
Passo 2
Pro eixo , somamos os momentuns dos fragmentos. Consideramos o momentum do terceiro fragmento, que queremos determinar. Pra isso, basta verificar os vetores na imagem e olhar seus valores no eixo . Vamos ter:
Assim:
Passo 3
Fazemos a mesma coisa pro eixo . Teremos como o momentum do terceiro fragmento no eixo . Olhamos na imagem os valores dos momentuns no eixo e determinamos:
Assim:
Resposta
e