Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 54
Uma onda plana de luz monocromática incide normalmente em um filme fino de óleo de espessura uniforme que cobre uma placa de vidro. É possível fazer variar continuamente o comprimento de onada da fonte luminosa. Uma interferência destrutiva da luz refletida é observada para comprimentos de onda de e e para nenhum outro comprimento de onda dentro deste intervalo. Se o índice de refração do óleo é e o do vidro é , determine a espessua do filme de óleo.
Passo 1
A questão trata sobre interferência em filmes finos. Um esquema que ilustra o filme de óleo é mostrado na figura:
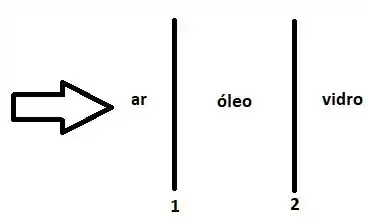
Como e , vai ocorrer inversão de fase nas duas reflexões, de modo que podemos desconsiderar isso:
Por outro lado, sabemos que
Passo 2
Para que a interferência seja destrutiva:
Assim,
Passo 3
Para , temos que
Já para :
Igulando as duas espessuaras:
Como não existe interferência destrutiva entre esses comprimentos de onda, temos que já que eles devem ser consecutivos:
Logo,
Assim,