Uma onda transversal senoidal é gerada em uma extremidade de uma longa corda horizontal por uma barra que se rnove para cima e para baixo ao longo de uma distância de . O movimento é contínuo e repetido regularmente vezes por segundo. A corda tem uma massa específica linear de e é mantida sob uma tensão de . Determine o valor máximo (a) da velocidade transversal e (b) da componente transversal da tensão .

(c) Mostre que os dois valores máximos calculados ocorrem para os mesmos valores da fase da onda. Qual o deslocamento transversal da corda nessas fases? (d) Qual é a taxa máxima de transferência deenergia ao longo da corda? (e) Qual o deslocamento transversal quando a taxa máxima de transferência de energia ocorre? (1) Qual e a taxa mínima de transferência de energia ao longo da corda? (g) Qual é o deslocamento transversal quando a

taxa de transferência dc energia mínima?

(b)Aqui, vamos olhar para um pedacinho da corda, que faz um ângulo igual a com o eixo , como mostra a figura:

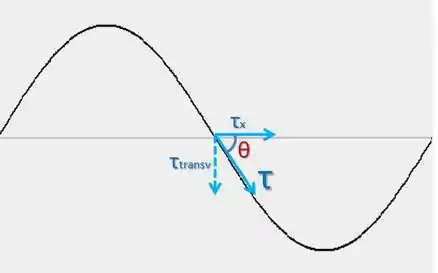
Queremos encontrar o valor máximo da componente transversal da tensão , igual a

Mas como? Para isso, como é consante e igual a , precisamos encontrar o valor máximo de , que corresponde a um máximo. Vamos apelidá-lo de .

Primeiro, perceba que, como a tensão é tangente à corda, a tangente do ângulo que ela faz com a horizontal é igual ao coeficiente angular da reta tangente à corda, que vale:

Como o máximo valor que um cosseno pode atingir é , segue que o máximo valor da tangente do ângulo é igual a

Estamos bem perto de encontrar . Como já sabemos quem é , só nos falta encontrar . Mas o valor dele sai diretamente do fato de que

A velocidade a gente encontra através da conhecida relação: :

Então pronto! Já podemos calcular o tal do e, consequentemente o querido :

O último passo agora é encontrar a máxima por meio da relação que vimos anteriormente :

(c)Lembremos, novamente, que a componente transversal da tensão é igual a

Vamos considerar aqui que é pequeno o suficiente para que

Nesse caso, a componente transversal da corda que a “puxa” para cima é igual a

Note que o valor máximo de é alcançado quando . Além disso, a velocidade da onda é igual a . Olha só, ela também atinge seu valor máximo quando . Isso mostra o que a alternativa (c) nos pede: “os dois valores máximos calculados ocorrem para os mesmos valores da fase da onda”.

(d)Considere agora um ponto localizado sobre a corda, que se desloca de uma distância igual a . Nesse caso, a tensão exerce um trabalho igual a . Com relação à potêcia, lembra da definição dela? Ela é igual à taxa temporal de geração de trabalho :

Uma coisa importante já podemos observar aqui:

A potência atinge seu valor máximo quando e atingem seus valores máximos! Fomos espertos e já calculamos esses valores nos passos anteriores. Eles valem

Então, a potência máxima já nos cai de bandeja aqui:

(e)No passo 3 vimos que quando a tensão transversal e a velocidade transversal atingem seus valores máximos. Mas quando , . Como , então nesse caso.

(f)Como vimos no passo 4, . Então, quando a tensão e a velocidade transversal são nulas, a potência também é nula.

(g)A taxa de transferência de energia, que vale é mínima quando a tensão e a velocidade transversais são mínimas, ou seja, quando . Mas isso ocorre quando e, consequentemente, .

Então, como , segue que o deslocamento vertical da corda é dado por .