Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Questões Conceituais - Ex. 1
Ordene em sequência decrescente os momentos de a e correspondentes aos objetos da FIGURA Q9.1.
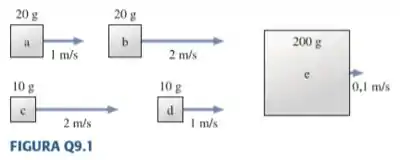
Passo 1
Para ordenarmos os momentos de cada bloco, vamos primeiro calcular eles para cada caso:
Substituindo para o bloco :
Para o :
Para :
Para :
E para :
Podemos ver que e são iguais, e na hora de ordenar não faz diferença quem vem primeiro.
Passo 2
Dos momentos acima de 5 objetos, o momento do objeto b é maior, os momentos do objeto a, c e “e”, são iguais, e o d tem o momento menor.
Portanto, a ordem do momento dos objetos do maior para o menor é
Resposta
Exercícios de Livros Relacionados
Uma bola de aço de 3,00k g bate em uma parede com velocidade de 1 0,0m / s a um ângulo de θ=60,0 ° com a superfície. Ela quica e recua com a mesma velocidade e mesmo ângulo (Fig. P8.9). Se a bola esti
Em um jogo de softball, uma bola de 0,200k g cruza a mesa a15,0m / s a um ângulo de 45,0 º º abaixo da horizontal. O batedor bate na bola em direção ao centro do campo, proporcionando uma velocidade d
Há (pode-se dizer) três teorias igualmente importantes de movimento para uma partícula isolada: a Segunda Lei de Newton, que afirma que a força total sobre a partícula causa sua aceleração; o teorema
O ângulo descrito por uma unidade de disco girando é dado θ t = a + b t - c t 3 , onde a , b e c são constantes positivas tais que se t for dado em segundos, θ deve ser medido em radianos.Quanto t = 0
A velocidade angular de um volante obedece à equação ω z t = A + B t 2 , onde t está em segundos e A e B são constantes, com valores numéricos de 2,75( p a r aA ) e 1,5( p a r aB ) . a) Quais são as u