Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.6 - Ex. 27
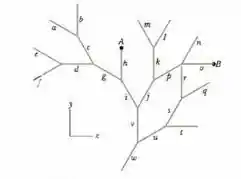
Para se orientarem, as formigas de jardim costumam ciar uma rede de trilhas marcadas por feromônios. Partindo do formigueiro, cada uma dessas trilhas se bifurca repetidamente em duas trilhas que formam um ângulo de . Quando uma formiga perdida encontra uma trilha, pode saber em que direção fica o formigueiro ao chegar ao primeiro ponto de bifurcação. Se estiver se afastando do formigueiro, encontrará duas trilhas que formam ângulos pequenos com a direção em que estava se movendo, para a esquerda e para a direita. A figura mostra uma rede de trilhas típica, com segmentos de reta de de comprimento e bifurcações simétricas de Trajetória v é paralela ao eixo Determine (a) o módulo e (b) o ângulo (em relação ao semieixo positivo) do deslocamento até o formigueiro (encontre-o na figura) de uma formiga que entra na rede de trilhas no ponto Determine (c) o módulo e (d) o ângulo de uma formiga que entra na rede de trilhas no ponto
Passo 1
Quanta dificuldade para um simples formigueiro não é mesmo? Enfim, de bater o olho podemos dizer que devido o ponto estar situado na extremidade desse jogo de linhas é por ele que o formigueiro começa. Logo, seu ângulo pedido em (a) é de , pois o ponto é perpendicular com o plano cartesiano.
Passo 2
Continuando com a resolução de (a), partindo do ponto A o primeiro deslocamento é de:
Depois de ter completado o primeiro trajeto vamos para o próximo ponto. O tracinho exerce 30° com a vertical certo? Então vamos decompo-lo dessa maneira:
***Nota de rodapé que não é rodapé: Como estamos adotando o ângulo em relação a vertical, usamos seno para o eixo x e cosseno para o eixo y.
Passo 3
Continuando nossa longa jornada, na próxima parada precisamos calcular o deslocamento em , como ele está perpendicular com o plano sabemos que o deslocamento é de:
Nossa última parada é o palitinho , nele temos a mesma angulação de 30° com a vertical que foi vista no palitinho , assim o valor do vetor é o mesmo, apenas com o valor negativo devido sua posição.
Passo 4
Agora que obtivemos todos os valores, devemos somá-los e calcular seu módulo para terminarmos de responder (a).
Passo 5
Para resolver (b) tudo fica mais simples pois as contas são as mesmas já que os palitos possuem mesmas angulações entre si. O primeiro ponto partindo de B possui um deslocamento de :
Partindo ao próximo ponto, observamos aquela mesma angulação de 30° e cuidando com o sinal sabemos que os dois valores serão negativos devido sua disposição.
Em seguida aparece o traço que possui valor de deslocamento de:
Passo 6
Partindo para o fim de nossa caminhada nesse Reality Show: “Um dia como uma formiga”. Chegamos ao palito novamente, que como já visto antes vale:
Obtendo todos os deslocamentos proposto, vamos calcular por fim seu módulo e meter o pé desse formigueiro.
Além disso, o ângulo pedido pode ser calculado pela inversa da tangente nesse caso, utilizando os vetores unitários do deslocamento total.