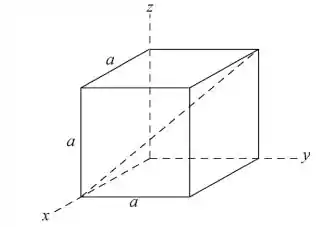
Na Fig. 3.30, um cubo de aresta a tem um dos vértices posicionado na origem de um sistema de coordenadas . A diagonal do cubo é uma reta que vai de um vértice a outro do cubo, passando pelo centro. Em termos dos vetores unitários, qual é a diagonal do cubo que passa pelo vértice cujas coordenadas são (a) (b) (c) e (d) ? (e) Determine os ângulos que as diagonais do cubo fazem com as arestas vizinhas. (f) Determine o comprimento das diagonais de cubo em termos de .

Da mesma forma que no item anterior , podemos observar que o ponto mais distante do vértice é o ponto . Podemos achar a diagonal através da relação :

Reparem o ponto mais distante do vértice é o ponto . Podemos achar adiagonal através da relação :

O vértice mais distante do ponto é o vértice . Dessa forma , Podemos achar adiagonal através da relação :

Então galera , a primeiracoisa quedevemos fazer é considerar o vetor que liga o vértice inferior esquerdo ao vértice superior direito, . Podemos pensar nesse vetor como a soma do vetor , paralelo ao eixo , com o vetor , perpendicular ao eixo . A tangente do ângulo entre o vetor e o eixo é a componente perpendicular dividida pela componente paralela. Como o módulo da componente perpendicular é e o módulo da componente paralela é . Assim, . O ângulo entre o vetor e as outras duas arestas vizinhas (os eixos e ) é o mesmo, o que também acontece com o ângulo entre os outros vetores diagonais e as arestas vizinhas a esses vetor.

O comprimento de qualquer umadas diagonais pode ser obtido através relação :

Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir 