Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.6 - Ex. 22
Um explorador polar foi surpreendido por urna nevasca, que reduziu a visibilidade a praticamente zero, quando retornava ao acampamento. Para chegar ao acampamento, deveria ter caminhado para o norte, mas, quando o tempo melhorou, percebeu que na realidade havia caminhado em uma direção ao norte do leste. (a) Que distância e (b) em que sentido deve caminhar para voltar à base?
Passo 1
Para resolver este tipo de problema é preciso lembrar que para somar dois vetores podemos obter as componentes escalares dos vetores e, em seguida, combiná-las, eixo por eixo, com isso obtemos as componentes do vetor soma e escrevendo as componentes usando a notação de vetores unitários podemos escrever o vetor resultante da soma. Logo:
Para isso, precisamos lembrar que, dado o módulo do vetor () e o ângulo que este faz com o semieixo positivo (), podemos escrever suas componentes da seguinte maneira:
Beleza?!
Não menos importante, devemos nos lembrar que o módulo de um vetor é dado por:
E o ângulo medido em relação ao semieixo positivo é dado por:
Neste problema nós conhecemos o módulo de dois vetores ( e ) e dois sentidos ( está a norte do ponto de partida e a ao norte do leste também do ponto de partida) e precisamos determinar a distância que o explorador deve caminhar para chegar ao ponto (acampamento) e o sentido deste deslocamento.
Para facilitar a interpretação, vamos fazer uma ilustração com auxílio do plano cartesiano e já representaremos o vetor que desejamos determinar, beleza?
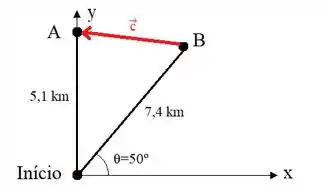
Portanto, para determinar a distância que o explorador deve caminhar para chegar no acapamento devemos fazer a soma vetorial da distância que ele deveria percorrer e da distância que ele percorreu.
Passo 2
Para determinar as componentes escalares do vetor utilizaremos as equações explicitas acima, porém, é preciso perceber, através da ilustração que foi considerado neste problema o semieixo positivo partindo da origem no sentido norte, por isso o ângulo que o vetor faz com o semieixo positivo é , assim:
Para determinar as componentes escalares do vetor faremos de maneira análoga:
Passo 3
Reescrevendo a soma vetorial dada no enunciado:
Agora, somamos as componentes eixo por eixo:
Portanto, podemos fazer a combinação dessas componentes de para escrever o vetor em termos dos vetores unitários:
Passo 4
Para encontrar a distância que o explorador deve percorrer devemos calcular o módulo do vetor usando a equação explicitada no passo :
Passo 5
Para determinar o ângulo que o vetor faz com o semieixo positivo também usaremos a equação explicitada no passo :
Devemos tomar cuidado quando utilizando a função na calculadora, pois dois ângulos e possuem o valor. Assim, precisamos determinar em qual quadrante o nosso vetor está a partir da análise do sinal das componentes.
Como nosso vetor possui a componente e a componente positivas, então este só pode estar no primeiro quadrante, pois é o único cujo o seno e cosseno são positivos, portanto:
Resposta
- ;
- .