Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 4.Problemas - Ex. 1

Um par de cargas puntiformes + 2 q e - q estão separadas por uma distância l . Mostre que a superfície equipotencial V = 0 é uma esfera e determine o seu centro e raio.

Passo 1

Se liga! Queremos encontrar a superfície onde a soma dos potenciais correspondentes as cargas + 2 q e - q seja nula. Vou estipilar o ponto P x , y , z sendo o ponto onde o potencial se nula. Olha a figura!

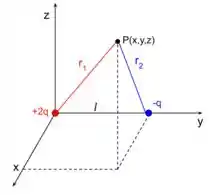
Podemos escrever o potencial gerado por uma carga Q num ponto à uma distância d como

V = k Q d

Se chamarmos de V 1 o potencial da carga + 2 q e V 2 o da carga - q , teremos

V 1 = k 2 q x 2 + y 2 + z 2

V 2 = k - q x 2 + ( y - l ) 2 + z 2

Passo 2

Já que queremos o ponto onde o potencial é nulo, basta somar V 1 e V 2 e igualar a zero.

k 2 q x 2 + y 2 + z 2 + k - q x 2 + ( y - l ) 2 + z 2 = 0

k q 2 x 2 + y 2 + z 2 - 1 x 2 + ( y - l ) 2 + z 2 = 0

Como o produto k q não pode ser zero, temos

2 x 2 + y 2 + z 2 = 1 x 2 + ( y - l ) 2 + z 2

Agora precisamos melhorar isso, certo?!

Passo 3

Multiplicando cruzado e elevando a quadrado, teremos

x 2 + y 2 + z 2 = 4 x 2 + ( y - l ) 2 + z 2

Podemos melhorar mais um pouquinho

3 x 2 + 3 y 2 + 3 z 2 - 8 y l + 4 l 2 = 0

Podemos dividir tudo por 3

x 2 + y 2 + z 2 - 8 l 3 y + 4 l 2 3 = 0

Agora vamos fazer mais um ajuste usando um artifício de completar quadrado para o y.

( x - 0 ) 2 + y - 4 l 3 2 + ( z - 0 ) 2 - 16 l 2 9 + 4 l 2 3 = 0

Olha o que encontramos?

( x - 0 ) 2 + y - 4 l 3 2 + ( z - 0 ) 2 = 2 l 3 2

Essa é a equação de uma circunferência de centro

0 , 4 l 3   , 0

e raio

2 l 3 .

Resposta

  P o s i ç ã o   d o   C e n t r o :   0 , 4 l 3   , 0

R a i o   i g u a l   a :     2 l 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eletricista foi eletrocutado por acidente e numa reportagem jornalística afirmou-se que: “Ele tocou acidentalmente num cabo de alta tensão e 20.000V de eletricidade atravessaram seu corpo.” Critiqu
Faça a distinção entre diferença de potencial e diferença de energia potencial. Dê exemplos usando cada termo com adequação.
Conhecendo-se o campo E em um só ponto, podemos calcular V no mesmo ponto? Se não, que informações a mais são necessárias?
Os conselhos dados a alpinistas apanhados em tempestades acompanhadas de trovões e raios são: (a) abandonar rapidamente os picos e (b) juntar os pés e agachar-se num descampado, somente os pés tocando
Se E for nulo num ponto, deverá V também ser nulo em tal ponto? Dê alguns exemplos que justifiquem sua resposta.