Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 12

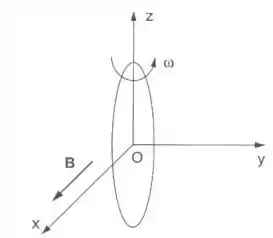
Uma espira circular de raio a , auto-indutância L e resistência R gira em torno do eixo z , com velocidade angular constante ω , num campo magnético uniforme B → .

a) Calcule a fem E e a corrente I induzida na espira, em regime estacionários (após um tempo longo).

b) Calcule o vetor momento de dipolo magnético m → correspondente.

c) Obterna o torque (vetor) τ → correspondente sobre a espira.

Passo 1

Vamos tentar entender o que está acontecendo! Temos um campo magnético externo B → na direção x ^ :

B → = B   x ^

Como a espira gira em torno do eixo z , seu vetor normal é perpendicular a esse eixo e “gira” no plano x y com velocidade angular ω . Assim, podemos escrever

n ^ = cos ⁡ ω t   x ^ + s e n   ω t   y ^

O fluxo magnético sobre a espiro devido ao campo externo é:

Φ = ∫ B → ⋅ d A → = ∫ B   x ^ ⋅ cos ⁡ ω t   x ^ + s e n   ω t   y ^   d A = B cos ⁡ ( ω t ) ⋅ A

Como A = π a 2 , temos que

Φ = B π a 2 cos ⁡ ω t

Esse fluxo é variável no tempo. Portanto, ele deve induzir uma fem!

Passo 2

Da lei de Faraday, temos que

E = - d Φ d t

Portanto,

E = - - B π a 2   ω   s e n   ω t

Ou ainda,

E = ω B π a 2   s e n ω t

Note que se trata de uma fem alternada, de modo que é conveniente escrever

E t = E 0   s e n   ω t = E 0 cos ⁡ ω t - π 2 ,

onde

E 0 = ω B π a 2

Quis escrever em termos do cosseno para que a fem física seja a parte real da fem complexa:

E ^ = E 0   e i ω t - π 2

Passo 3

Para obtermos a fem induzida, não consideramos a autoindutância pois o campo externo é o responsável por induzi-la. Já para achar a corrente induzida, temos que considerar a autoindutância.

A impedância da espira é dada por

Z = R + i   ω L

Note que R é a resistência elétrica e ω L é a reatância indutiva. Vamos aplicar a lei de Ohm:

E ^ = Z   I ^

Assim,

E 0   e i ω t - π 2 = R + i   ω L   I ^

Vamos escrever I ^ = I 0   e i ω t + ϕ . Assim,

E 0   e i ω t   e - i π 2 = R + i   ω L   I 0   e i ω t   e i ϕ

Com isso,

I 0   e i ϕ + π 2 = E 0 R + i   ω L

Note que podemos escrever

E 0 R + i   ω L = E 0 R + i   ω L ⋅ R - i   ω L R - i   ω L = E 0   R - i   ω L R 2 + ω 2 L 2

Logo,

I 0   e i ϕ + π 2 = E 0   R 2 + ω 2 L 2   R - i   ω L

Passo 4

Calculando o módulo de R - i   ω L , temos que

R - i   ω L = R 2 + ω 2 L 2

Assim,

I 0 = E 0   R 2 + ω 2 L 2   R - i   ω L = E 0 R 2 + ω 2 L 2

Para achar a fase, temos que

tan ⁡ ϕ + π 2 = - ω L R ⇒ ϕ + π 2 = arctan ⁡ - ω L R

Como o arcotangente é uma função ímpar:

ϕ = - π 2 - arctan ⁡ ω L R = - π 2 - ϕ L ,           ϕ L = arctan ⁡ ω L R

Como I ^ = I 0   e i ω t + ϕ e a corrente física é a parte real de I ^ :

I t = I 0 cos ⁡ ω t + ϕ

Logo,

I t = I 0 cos ⁡ ω t - ϕ L - π 2 = I 0   s e n   ω t - ϕ L

Assim, a corrente induzida é

I t = π a 2 B ω R 2 + ω 2 L 2   s e n   ω t - ϕ L ,           ϕ L = arctan ⁡ ω L R

Passo 5

No item (b) queremos calcular o momento de dipolo magnético m → . Sabemos que ele é dado por

m → = ∫ I   d A → = I A   n ^

Portanto,

m → = I π a 2   n ^

Mas sabemos que

n ^ = cos ⁡ ω t   x ^ + s e n   ω t   y ^

Portanto, o momento magnético é

m → = I π a 2   cos ⁡ ω t   x ^ + s e n   ω t   y ^

Passo 6

Por fim, no item (c), queremos calcular o torque sobre a espira. Para um momento magnético m → num campo B → , o torque é

τ → = m → × B →

Portanto,

τ → = I π a 2   cos ⁡ ω t   x ^ + s e n   ω t   y ^ × B   x ^

Com isso,

τ → = - I π a 2 B   s e n   ω t   z ^

Podemos escrever ainda,

τ → = - I E ω   z ^

Resposta

E = ω B π a 2   s e n ω t

I t = π a 2 B ω R 2 + ω 2 L 2   s e n   ω t - ϕ L ,           ϕ L = arctan ⁡ ω L R

m → = I π a 2   cos ⁡ ω t   x ^ + s e n   ω t   y ^

τ → = - I π a 2 B   s e n   ω t   z ^ = - I E ω   z ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

QUENCHING EM UM ÍMÃ DE R M . Ímãs transportando correntes muito grandes são usados para produzir os campos magnéticos uniformes e intensos necessários para os exames por ressonância magnética ( R M ).
(Casamento de impedâncias) No circuito da figura ,Z=R+i X é a impedância interna do gerador de corrente alternada de voltagem VeZ '=R '+i X ´ a impedância alimentada pela corrente I do gerador. Demons
Desejamos enrolar uma bobina de modo que ela tenha resistência, mas essencialmente nenhuma indutância. Como fazer isso?
Um solenoide e enrolado com uma única camada de fio de cobre isolado (diâmetro = 2.5 mm). Ele tem 4 cm de diâmetro e um comprimento de2 m. (a) Quantas espiras possui o solenoide? (b) Qual é a indutânc
A corrente num circuito RL cai de 1 A para 10 mA no primeiro segundo após a remoção da bateria do circuito. Sendo L = 10 H, calcule a resistência R do circuito.