Uma paraquedista confia na resistência do ar (principalmente no seu paraquedas) para diminuir sua velocidade durante a queda. Sabendo que sua massa, incluindo a do paraquedas, é igual a e que a resistência do ar exerce uma força de baixo para cima de sobre ela e seu paraquedas,

1. Qual é o peso da paraquedista?
2. Desenhe um diagrama de corpo livre para a paraquedista (veja seção ). Use esse diagrama para calcular a força resultante sobre a paraquedista. A força resultante é orientada de baixo para cima ou de cima para baixo?
3. Qual é a aceleração (módulo e direção) da paraquedista?

a) Bom... Aqui temos um paraquedista caindo, então vamos calcular essa força peso sobre ele.

O módulo da força peso é a multiplicação da massa pela aceleração da gravidade. Na Terra e a massa da paraquedista é então a força peso é:

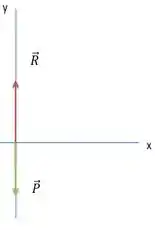
b) As duas forças que agem sobre a pessoa durante a queda são a força peso verticalmente para baixo e a força de resistência do ar verticalmente para cima.

O peso está representado em verde e a resistência em vermelho:

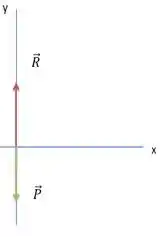
A força resultante vai ser a soma de todas as forças que agem sobre a pessoa. Com a força peso está para baixo, ela entra negativa nessa soma.

Temos que todas as forças agem só na vertical, no eixo . Sendo assim temos:

Temos uma força resultante de módulo que aponta para cima! (já que ela é positiva)

c) Usando a Segunda Lei de Newton podemos descobrir a aceleração da paraquedista:

Onde é a força resultante, é a massa e é a aceleração.

Substituindo os nossos dados:

Sendo assim a aceleração é para cima.