Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 38

1,5 m / s (figura 4.37 ). Quando o navio está a 500 m do recife, o vento cessa e os motores voltam e funcionar. O leme está emperrado, e a única alternativa é tentar acelerar diretamente para trás, para se afastar do recife. A massa do navio e da carga é de 3,6 × 10 7 k g , e os motores produzem uma força horizontal de 8 × 10 4 N sobre o navio. Ele atingirá o recife? Se sim, o petróleo estará seguro? O casco resiste ao impacto de uma velocidade escalar de até 0,2 m / s . Ignore a força retardadora de água sobre o casco do navio-tanque.

Passo 1

Esse problema parece complicado, mas vou ajudar você a resolvê-lo, vamos lá?

Temos aqui um problema que envolve a segunda lei de Newton e ao mesmo tempo, as equações do MRUV.

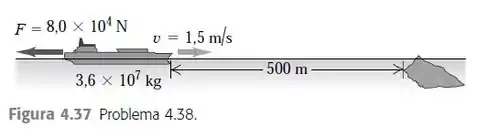
O navio se desloca para a direita com velocidade de 1,5 m / s e está 500 m distante de um recife. Para evitar o choque e o vazamento de óleo (o que seria terrível não só para a empresa, mas principalmente para os bichinhos que vivem no mar) o comandante aciona os motores com força total para a esquerda, a fim de diminuir ao máximo a velocidade do navio.

Sabendo a aceleração do navio (via segunda lei), podemos descobrir qual a distância que ele tem que percorrer até parar completamente (via MRUV). Se for menor do que 500 m , o navio não se choca com o recife. Se for maior, sim.

E se for maior, podemos usar as equações do MRUV e determinar a velocidade com que o navio atinge o tanque e saber se os bichinhos estarão a salvo ou não. Vamos lá?

Passo 2

Primeiro vamos descobrir a aceleração via segunda lei. Newton nos diz que a força resultante que age sobre um corpo é proporcional ao produto de sua massa pela aceleração que ele sofre:

F r = m ⋅ a

A massa do navio é 3,6 × 10 7 k g e a força resultante vale - 8 × 10 4 N , agora é só substituir:

a = - F r m = - 8 × 10 4 3,6 × 10 7 = - 2,22 × 10 - 3 m / s 2

Passo 3

Beleza! Agora que temos a aceleração, vamos descobrir a distância Δ x necessária para parar completamente esse navio. Da equação de Toriccelli:

v 2 = v 0 2 + 2 a Δ x

0 2 = 1,5 2 + 2 . - 2,22 × 10 - 3 . Δ x

Δ x = -   1,5 2 2 . - 2,22 × 10 - 3 = 506,25 m

Opa! O navio bate sim no recife!

Agora precisamos descobrir com qual velocidade!

Passo 4

Usando a mesma fórmula, mas agora para determinar v sendo Δ x = 500 temos:

v 2 = 1,5 2 + 2 . - 2,22 × 10 - 3 . 500

v = 0,0289 = 0,17 m / s

Ufa! O problema nos diz que o casco do navio suporta um impacto de velocidade até 0,20 m / s . Então o óleo está a salvo! (e os bichinhos também!).

Resposta

S i m . S i m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23 . || O cachorro da F I G U R AP 7.23 arrasta os trenós A e B sobre a neve. Os coeficientes de atrito dos trenós com a neve valem 0,10 . Se a tensão na corda 1 for de 150N , qual será o valor da ten
8 . || A F I G U R AE X 7.8 mostra dois ímãs potentes localizados nas superfícies opostas de uma pequena mesa. A força atrativa de ação a distância entre eles mantém o ímã inferior no lugar. a . Desen
16 . | Uma corda de 2,0k g está pendurada no teto de uma casa. Quanto vale a tensão no ponto médio da corda?
18 . || O bloco B da F I G U R AP 7.18 repousa sobre uma superfície para a qual os valores dos coeficientes de atrito estático e cinético valem, respectivamente, 0,60 e 0,40 . As cordas são de massas
8 . || A F I G U R AE X 7.8 mostra dois ímãs potentes localizados nas superfícies opostas de uma pequena mesa. A força atrativa de ação a distância entre eles mantém o ímã inferior no lugar. a . Desen