Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.8 - Ex. 42
Uma partícula alfa (núcleo de um átomo de hélio) tem uma massa de e uma carga de . Determine (a) o módulo e (b) a direção de um campo elétrico capaz de equilibrar o peso da partícula.
Passo 1
E aí, pessoal! 😁
Galera essa questão não tem mistério tá? O problema quer saber da gente qual é o campo elétrico capaz de equilibrar o peso da partícula. Pra te falar a real o campo elétrico sozinho não equilibra nada, quem equilibra é a força elétrica, só que ela depende do campo, se liga aí.
Vamos desenhar o diagrama de corpo livre da partícula pra gente ver as forças que atuam nela.
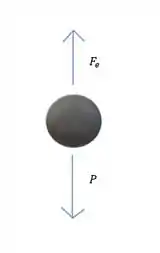
Aqui temos a força elétrica atuando na direção oposta ao peso para equilibrar a partícula e isso já responde o item b, já que o campo elétrico se propaga na mesma direção da força. pra resolvermos o problema vamos aplicar a condição de equilíbrio no eixo
Veja só! 😊
Passo 2
Fazendo o equilíbrio das forças temos o seguinte:
E como:
Temos:
E aqui vamos isolar esse campo que é suficiente pra que a força elétrica se iguale a força peso.
Lembrando que a carga dessa partícula alfa é :
Agora, só falta substituir os valores e correr pro abraço.
E como dissemos lá no passo 1. A força deve ser para cima para equilibrar o peso e o campo elétrico segue essa mesma direção.
E aí! entendeu tudo? Responde Aí! 😬
Resposta
Letra (a):
Letra (b): Vertical para cima