Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 98

Partindo de uma estação, um trem de metrô acelera a partir do repouso à taxa constante de 1,00 m/s² na metade do percurso até a estação seguinte, e depois freia à mesma taxa no resto do percurso. A distância total entre as estações é 900 m. (a) Esboce um gráfico da velocidade v x como função do tempo para todaa viagem. (b) Esboce um gráfico da posição como função do tempo para toda a viagem. Coloque valores numéricos apropriados nos dois eixos.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para esboçar o gráfico solicitado no item (a), precisamos saber o tempo de metade da viagem:

∆ x = v 0 ∆ t + 1 2 a ∆ t 2

Como v 0 = 0 , temos:

∆ x = 1 2 a ∆ t 2

∆ t = 2 ∆ x a

Substituindo os valores, temos:

∆ t = 2 ⋅ 450 1  

∆ t = 30   s

A função que rege a curva do movimento é:

v t = v 0 + a t

v t = t

Logo, o nosso gráfico terá este formato:

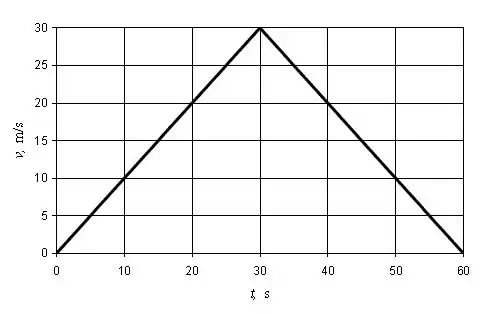
Passo 2

O gráfico da posição como função do tempo, pode ser obtido pela equação:

x t = 1 2 a t 2

Logo, o nosso gráfico terá este formato:

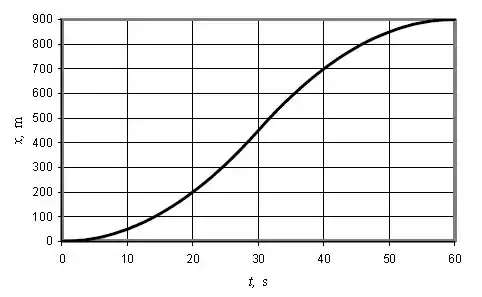
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A FIGURA P2.38 mostra um conjunto de gráficos cinemáticos para uma bola que rola sobre um trilho. Todos os trechos do mesmo são retilíneos, mas alguns podem ser inclinados. Desenhe uma figura do trilh
Desenhe gráficos da posição, da velocidade e da aceleração da bola mostrada na FIGURA P2.37. Consulte o Problema 35 para informação adicional. A direção da bola varia, mas não ocorre qualquer redução
Uma bola rola sobre o trilho livre de atrito mostrado na FIGURA P2.35. Cada trecho do trilho é reto, e a bola passa suavemente de um trecho para outro, sem que sua rapidez seja alterada e sem sair do
A FIGURA P2.39 mostra um conjunto de gráficos cinemáticos para uma bola que rola sobre um trilho. Todos os trechos do mesmo são retilíneos, mas alguns podem ser inclinados. Desenhe uma figura do trilh
Um objeto parte do repouso em x =0m no instante t =0s . Cinco segundos depois, em t = 5,0s , o objeto é observado em x =40,0m e com velocidade v x = 11m / s .a. A aceleração do objeto foi uniforme ou