Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 50
50. Uma pedra é atirada para cima, a um ângulo de 53° com a horizontal. A altura máxima que ela atinge, acima do ponto de lançamento, é . Qual a rapidez inicial da pedra? Despreze a resistência do ar.
Passo 1
Bom, esse é um clássico exemplo de lançamento oblíquo, que vai ter a seguinte cara mostrada na imagem abaixo.
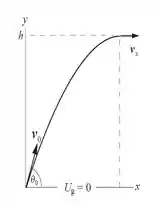
Antes de começar a debater sobre o que fazer para resolver essa questão, vamos primeiro definir a origem do nosso referencial gravitacional , como sendo o solo.
Agora, que já cumprimos o primeiro mandamento das questões sobre trabalho e energia, vamos dar início ao nosso raciocínio. Bom! O exercício diz que a altura máxima atingida é . Lá da cinemática, no lançamento oblíquo de projéteis, vimos que nessa condição de altura máxima apenas a componente horizontal da velocidade de lançamento está presente. O que isso quer dizer?
Isso mesmo, a incógnita velocidade inicial irá aparecer nas condições iniciais e finais de nosso cálculo. É claro que como a resistência do ar é desprezada, não precisa nem dizer que há conservação de energia.
Passo 2
Uma vez que a energia é conservada a energia mecânica no lançamento da pedra é igualzinha a energia mecânica na condição em que a pedra atinge sua altura máxima .
Bom, é meio óbvio que o único tipo de energia presente no começo do lançamento é a cinética. Mas e na altura máxima , que tipo de energias existem?
Bem, como descrito no , na altura máxima a pedra ainda tem uma velocidade , que é dada como a componente horizontal da velocidade de lançamento e igual a:
Logo, na altura máxima estão presentes energia potencial gravitacional e cinética. Igualamos, então as energias potencial gravitacional e cinética final e e cinética inicial :
Passo 3
Obtida, a relação que queremos entre as energias, basta então, desenvolvê-la:
Substituem-se os valores numéricos correspondentes, dado que
Resposta
A rapidez inicial da bola é igual a .