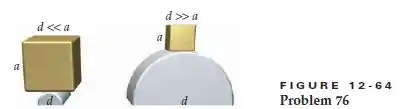
Um cubo maciço de aresta a, equilibrado sobre um cilindro de diâmetro d, está em equilíbrio instável se (Figura 12-64), e está em equilíbrio estável se . O cubo não escorrega sobre o cilindro. Determine o menor valor da razão para o qual o cubo está em equilíbrio estável.

Vamos lá ! Esta questão é mais teórica e vai envolver alguns conceitos de rotação de corpos rígidos.

Bom, nós temos o cubo que adicionado sobre um cilindro, vamos considerar que houve um pequeno deslocamento rotacional, δθ do cubo, movendo-se do equilíbrio em que se encontrava para uma nova posição.

Vamos ilustrar isso com uma figura:

Quando isso acontece o ponto de contato entre o cubo e o cilindro vai se deslocar de R para R.δθ (aqui entra nossa compreensão sobre a rotação dos corpos!), onde . Como resultado desse movimento, o cubo é girado através no mesmo ângulo δθ e, portanto, seu centro (+) é deslocado na mesma direção por um fator de .

Se o deslocamento do centro de massa do cubo for menor que o do ponto de contato, o torque sobre o ponto de contato é um torque de restauração e o cubo retornará à sua posição de equilíbrio. Se, por outro lado, , então o torque sobre o ponto de contato devido a está na direção de δθ e fará com que o deslocamento do equilíbrio aumente.

Sendo assim:

Então o valor mínimo da razão é 1, para que ocorra um equilíbrio estável.