Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 37
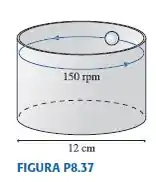
Uma pequena esfera de aço de rola de maneira que ela percorre a face interna de um cilindro de aço vertical. O cilindro, mostrado na FIGURA , tem de diâmetro. Considere que a resistência de rolamento seja suficientemente pequena para que a esfera efetue por vários segundos. Durante este tempo, a esfera descreverá um círculo horizontal, a uma altura constante, ou descreverá uma trajetória espiralada para baixo, dentro do tubo?
Passo 1
Olá, tudo bem?
Essa bolinha vai manter a altura ou descrever uma trajetória em espiral para baixo dependendo da relação entre o valor da força de atrito e do peso .
Se tivermos , então a força de atrito estático máxima não é suficiente para suportar a bolinha e ela irá espiralar para baixo.
Na vertical temos a força de atrito (apontando para cima, já que o movimento seria para baixo) e para cima a força peso para baixo. Ao longo da direção radial temos a força normal, que surge do contato da bolinha com a parede do recipiente. Essa força deve ser igual à força centrípeta =)
Passo 2
Começando pelas equações na direção radial temos:
Aqui já coloquei a força centrípeta em termos da velocidade angular , pois esse dado nos foi fornecido no enunciado. Agora vamos olhar com mais carinho com para a velocidade angular. Temos que , mas precisamos desse valor em , então para transformar precisamos multiplicar esse fator por , certo?
Então a força normal é:
Passo 3
Agora vamos descobrir quanto vale a força de atrito:
E para saber se essa força é suficiente para suportar a bolinha, precisamos calcular a força peso e comparar. A força peso é:
Então comparando essas duas forças, temos que , logo é suficiente para que a bolinha se mantenha em linha reta durante as revoluções =)
Beleza?
Espero ter ajudado!
Vamos pra próxima?