Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 57
Um pequeno avião parte do ponto A para chegar a um aeroporto que está 520 km ao norte, no ponto B. A rapidez do avião no ar é de 240 km/h e há um vento constante de 50 km/h soprando diretamente para o sudeste. Determine para onde o avião deve apontar e o tempo de vôo.
Passo 1
Oi, pessoal, tudo bem? O avião vai se movimentar no ar, só que o ar está em movimento (na velocidade do vento). Quando temos um objeto que se move sobre algo que se move também é uma dica para gente pensar em termos de velocidade relativa.
Nesse tipo de questão, a primeira coisa é montar a equação da soma vetorial entre as velocidades presentes.
No nosso caso, a velocidade do avião em relação ao solo é a soma da velocidade do avião em relação ao vento com a velocidade do vento em relação ao solo :
E depois, o que a gente precisa fazer é esquematizar essa soma, entendendo quem são cada uma dessas velocidades. O esquema fica assim:
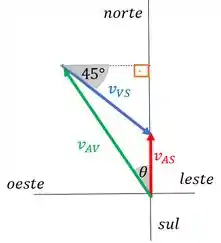
A velocidade do vento está sendo representada por e ela está fazendo um ângulo de com a horizontal porque a questão diz que ela aponta para a direção sudeste, que é a direção entre o Sul e o Leste. E ela vale .
A velocidade do avião em relação ao solo chamamos de (que dita a direção da trajetória) e ela aponta exatamente para o norte, que é pra onde a gente quer que o avião vá para poder chegar no ponto B, show?
E é a velocidade do avião em relação ao ar que vale . Aqui estamos supondo que o bico do avião faz um ângulo com a vertical e que a velocidade que ele tem em relação ao ar está nessa direção.
Aí você me pergunta, mas porque essa suposição? OHH, se liga, o vento está “soprando” na direção sudeste, se o bico do meu avião aponta na direção mostrada na figura, o vento irá modificar o movimento do avião de modo que ele consiga ir em direção ao aeroporto, sacou?
Depois de tudo isso, a gente vê o que a questão quer. Ela quer a direção da velocidade do avião em relação ao vento, ou seja, . E quer também o tempo de vôo. Bora lá descobrir!
Passo 2
Como a questão nos pergunta pra onde aponta o bico do avião, o que devemos descobrir é quem é esse ângulo .
Vimos que
Isso vale também só para as componentes das velocidades. Então a gente pode escrever:
Vamos escrever cada uma dessas componentes. Temos:
Porque essa velocidade é somente vertical. Temos também:
Seno porque é oposto ao eixo e o sinal de negativo porque essa velocidade está apontanto para o sentido negativo de . E por fim:
Cosseno porque esse ângulo de está colado num eixo paralelo ao eixo .
Passo 3
Aplicando para a direção a equação que relaciona esses três velocidades temos:
Então:
Para acharmos o ângulo teremos que aplicar a função inversa do seno:
Agora só precisamos substituir os valores dados na questão:
Substituindo os valores:
Passo 4
Para descobrir o tempo de vôo precisamos encontrar a velocidade do avião em relação ao solo, já que ela que rege nossa trajetória.
Para isso, vamos olhar para a direção do movimento e achar as componentes das velocidades nesse eixo e usar a equação da soma vetorial. Como está só na vertical, temos que:
E as outras a gente pode achar de forma análoga ao que fizemos para o eixo :
Aplicando para a direção a equação que relaciona as três velocidades:
Substituindo os valores dados na questão e :
Passo 5
Agora que sabemos a velocidade do avião com relação ao solo, podemos associar com a distância entre A e B para achar o tempo.
Resposta
no sentido anti horário a partir do norte. O tempo de vôo foi de 2,57 horas.