Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 54

Partindo do repouso no ponto A, você dirige sua moto até o ponto B, ao norte, distante 75,0 m, aumentando a rapidez a uma taxa constante de 2,00 m/s². Então você vai gradualmente virando para o leste ao longo de um caminho circular de 50,0 m de raio, com uma rapidez constante, de B até o ponto C, até que o sentido de seu movimento aponta para o leste, em C. Então você continua para o leste, resuzindo a rapidez a uma taxa constante de 1,00 m/s², até atingir o repouso no ponto D. (a) Quais são suas velocidade e aceleração médias m para a viagem entre A até D? (b) Qual é o seu deslocamento durante a viagem de A até C? (c) Qual a distância que você percorreu, em toda a viagem de A até D?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado descreve o passo a passo presente na imagem abaixo, e nos pede as velocidade e aceleração médias entre A e D.

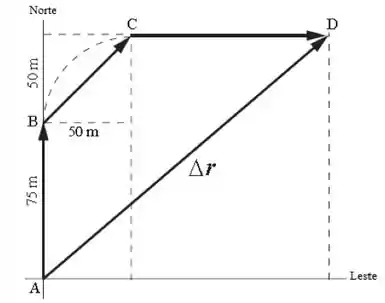
A velocidade média é dada por:

v → m é d = ∆ r → ∆ t

A posição pode ser estudada para cada momento:

∆ r → = ∆ r → A B + ∆ r → B C + ∆ r → C D

Utilizando as informações do enunciado, temos que:

∆ r → A B = 0 i ^ + 75 j ^

∆ r → B C = 50 i ^ + 50 j ^

∆ r → C D = ∆ r C D i ^

Para descobrir o deslocamento ∆ r C D , temos que:

∆ r C D = v C ∆ t C D + 1 2 a C D ∆ t C D 2

Sabemos que:

v C = v B = v A + a A B ∆ t A B

O tempo ∆ t A B é dado por:

∆ y A B = 1 2 a A B ∆ t A B 2

∆ t A B = 2 ∆ y A B a A B

∆ t A B = 2 ⋅ 75 2 = 8,66   s

Podemos então, encontrar a velocidade v C :

v C = 2 ⋅ 8,66   s

v C = 17,32   m / s

Sabemos que:

∆ t C D = ∆ v C D a C D = v D - v C a C D

∆ t C D = 0 - v C a C D

∆ t C D = - 17,32 - 1

∆ t C D = - 17,32   s

Então:

∆ r C D = 17,32 ⋅ 17,32 + 1 2 - 1 17,32 2

∆ r C D = 150   m

∆ r → C D = ( 150   m ) i ^

Logo:

∆ r → = ∆ r → A B + ∆ r → B C + ∆ r → C D

∆ r → = 0 i ^ + 75 j ^ + 50 i ^ + 50 j ^ + 150 i ^

∆ r → = 200 i ^ + 125 j ^

O tempo é dado por:

∆ t = ∆ t A B + ∆ t B C + ∆ t C D

Onde:

∆ t A B = 8,66   s

∆ t B C = 1 2 π r v B = 1 2 π ⋅ 50 17,32 = 4,535   s

∆ t C D = 17,32   s

Logo:

∆ t = 8,66 + 4,535 + 17,32

∆ t = 30,51   s

Passo 2

Podemos finalmente encontrar velocidade e aceleração médias.

A velocidade média é dada por:

v → m é d = ∆ r → ∆ t

v → m é d = 200 i ^ + 125 j ^ 30,51

v → m é d = ( 6,56   m / s ) i ^ + ( 4,10   m / s ) j ^

A aceleração média é dada por:

a → m é d = ∆ v → ∆ t = v → f + v → i ∆ t

a → m é d = 0 + 0 30 , 51

a → m é d = 0

Passo 3

O deslocamento de A até C é dado por:

∆ r → A C = ∆ r → A B + ∆ r → B C

Logo:

∆ r → A C = 75 j ^ + 50 i ^ + 50 j ^

∆ r → A C = 50 i ^ + 125 j ^

Passo 4

A distância total de A até D é dada por:

d t o t = d A B + d B C + d C D

d t o t = 75   m + 1 2 π ⋅ 50   m + 150   m

d t o t = 304   m

Resposta

a ) v → m é d = ( 6,56   m / s ) i ^ + ( 4,10   m / s ) j ^

a → m é d = 0

b ) ∆ r → A C = 50 i ^ + 125 j ^

c ) d t o t = 304   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade do projétil quando atinge sua altura máxima é a metade de sua velocidade na metade da sua altura máxima. Qual é o ângulo de projeção inicial do projétil?
Em t=0 , uma partícula que se move no plano x y com aceleração constante tem uma velocidade de v i →=( 3,00i ^–2,00j ^ )m / s e está na origem. Em t=3,00s , a velocidade da partícula é v f →=( 9,00i ^
Um peixe nadando em um plano horizontal tem v e l o c i d a d e i=( 4,00i ^+1,00j ^ )m / s em um ponto do oceano onde a posição relativa a uma determinada pedra é r i →( t )=( 10,0i ^–4,00j ^ )m . Apó
O pequeno peixe arqueiro (comprimento de 20c m a 25c m ) vive em águas salobras do sudeste da Ásia, entre Índia e Filipinas. Essa criatura, cujo nome é apropriado, captura sua presa atirando um jato d
Não é possível ver corpos muito pequenos, tais como vírus, utilizando um microscópio de luz comum. No entanto, em um eletrônico, podemos vê-los usando um feixe de elétrons em vez de um feixe de luz. A