Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.6 - Ex. 28
Uma pessoa puxa horizontalmente um bloco da figura , fazendo com que ambos os blocos movam-se juntos, como uma unidade. Para esse sistema em movimento, faça um diagrama do corpo livre claramente designado para o bloco , consderando que
- A mesa é livre de atrito e
-
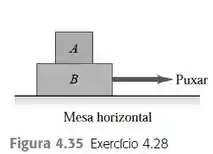
B e a mesa e a força de puxar é igual à força de atrito sobre o bloco , devido à mesa.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que desenhar o diagrama de corpo livre para o bloco
Vamos primeiro identificar as forças que estão agindo no nosso sistema. A primeira de todas é a gravitacional (em azul), que age em todos os corpos próximos à superfície terrestre. Essa força é direcionada verticalmente para baixo e age tanto no corpo , quanto no corpo .
A segunda força a ser considerada é a força de contato (em rosa), pois em ambos objetos, há sustentação, há o apoio deles em algum lugar, certo? O objeto está em contato com a mesa horizontal e o bloco está apoiado no corpo , então ambos possuem a força normal. Essa força é sempre perpendicular ao ponto de apoio.
Outra força a ser considerada é a força com que todo sistema é puxado (em preto)! É aquele “puxar” que tem ali na figura, vou chamar de força . Nesse caso, essa força é horizontal para direita e está sendo aplicado APENAS no bloco , como tá ilustrado ali na figura.
E mais uma forcinha existe nesse sistema! Ah! Sabe qual é? Vamos reler o enunciado: “fazendo com que ambos os blocos movam-se juntos, como uma unidade”, é essa parte aqui que estou interessada! Vamos pensar o seguinte: como os blocos movem-se juntos, eles não tem movimento relativo entre eles, certo? Isso quer dizer que não há deslizamento entre eles! Tá, mas você pode se perguntar mas o que isso implica, e eu te respondo: força de atrito entre eles! Eles só conseguem se manter juntos, sem deslizar um em relação ao outro, por conta do atrito entre os blocos (em verde)!
Aqui assumi que não há atrito entre a mesa e o bloco , mas se houvesse, teríamos de adicionar, beleza?
Aqui está um diagrama de forças dos dois blocos:
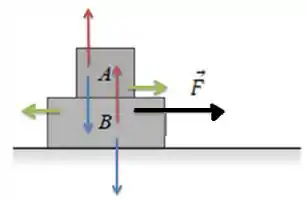
Agora deu! Essas são todas as forças que agem no sistema inteiro! Agora vamos ver o que o problema pede!
Passo 2
Na letra ele pede o diagrama de corpo livre para o bloco , então, dentre todas as forças existentes, quais são do bloco ? Revendo ali no passo anterior temos: a gravidade, a força normal e o atrito que o bloco faz no bloco . Mas e a força ? Não! Essa é aplicada apenas no outro bloco! E como não há atrito na mesa, teremos uma força resultante horizontal para a esquerda! Lembrem-se de que a força de atrito aponta sempre para o sentido oposto ao movimento relativo do objeto: quando o objeto é puxado, o objeto tende a ir para trás, certo? Então a força de atrito que o exerce sobre é para frente.
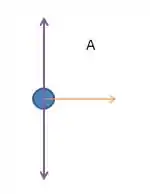
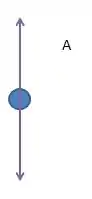
Assim podemos fazer o diagrama de corpo livre para
E faz sentido, não é? Todo sistema está se movimentando para a direita, logo devemos ter uma força resultante (em amarelo) para a dieita em todos os blocos, mesmo separadamente =)
Passo 3
Agora, no item b), o problema pede novamente o diagrama do corpo , mas agora com a presença da força de atrito entre a mesa e o bloco e ela é igual a força . Bom, agora não há mais força resultante para a direita, então os blocos movem-se com velocidade constante para a direita. Sendo assim, o diagrama pro corpo fica simplificado:
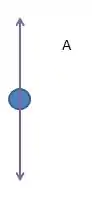E aí! o que achou? Responde Aí!
Resposta
