Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 37

As placas de um dispositivo de Thomson q / m têm 6,00   c m de comprimento e estão separadas por 1,20   c m . As extremidades das placas estão a 30,0   c m da tela do tubo. A energia cinética dos elétrons é 2,80   k e V . Se uma diferença de potencial de 25,0   V for aplicada entre as placas de deflexão, qual será o deslocamento do ponto onde o feixe de elétrons colide com a tela?

Passo 1

OPA OPA OPA, fala ae, tudo bem? Claro que está tudo bem ,afinal você está aqui,BUSCANDO conhecimento, vamos lá, sigamos firmes e SIMBORA PARA MAIS UMA QUESTÃO.

Primeiramente, vamos analisar a imagem abaixo para entender as deflexões que estão a ocorrer:

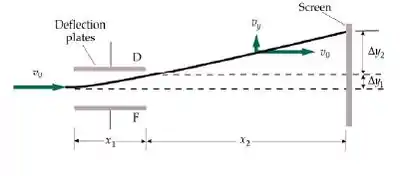
Observando a imagem podemos determinar o total de deflexões como a soma entre a deflexão que ocorre quando o feixe está entre as placas e aquela que ocorre quando o feixe se encontra no espaço aberto (LIBERDADE); Podemos usar equações com aceleração constante para representar cada uma das deflexões (empolga?), assim obteremos uma equação em termos de v 0 e E , podemos determinar o valor da velocidade inicial utilizando a Energia Cinética do feixe e o valor do campo elétrico a partir da diferença de potencial das placas e a distância entre elas, dessa forma poderemos determinar o quanto o ponto se deslocou no eixo y. (PEGOU A VISÃO BB? AGORA SENTE A PRESSÃO)

Let’s start!

Passo 2

Primeiro, vamos determinar o total de deflexões:

∆ y =   ∆ y 1 +   ∆ y 2

O nosso querido ∆ y 1 representa a deflexão (estamos usando muito essa palavra, hoje) do feixe enquanto está no campo elétrico e o ∆ y 2 é a deflexão (mais uma vez) do feixe quando está percorrendo o caminho fora do campo elétrico.

Determinando os termos:

∆ y 1 = 1 2 a y ∆ t 1 2 (1)

∆ y 2 = v y ∆ t 2 (2)

Temos que x 1 = v 0   ∆ t 1 , com isso, ∆ t 1 = x 1 v 0   , o tempo que um elétron está no campo elétrico entre as placas.

Agora vamos aplicar a segunda Lei de Newton para determinar a aceleração (OLHOS ABERTOS): q   E = m   a y →   a y = q E m , AGORA PODEMOS VER A VERDADEIRA FORMA DA EQUAÇÃO 1!

∆ y 1 = 1 2 a y ∆ t 1 2

∆ y 1 = 1 2 q E m x 1 v 0   2

Feito isto, vamos determinar v y , utilizando a y , teremos:

v y =   v 0 y +   a y   ∆ t y

v y =   0 +   q E m   x 1 v 0  

Substituindo na equação 2:

∆ y 2 = v y ∆ t 2

∆ y 2 = q E m   x 1 v 0   x 2 v 0  

∆ y 2 = q   E   x 1   x 2 m v 0 2  

Agora basta somas as duas deflexões e obter o valor do deslocamento!!!

Passo 3

Vamos iniciar somando as deflexões:

∆ y =   ∆ y 1 +   ∆ y 2

∆ y =   1 2 q E m x 1 v 0   2 +   q   E   x 1   x 2 m v 0 2  

∆ y =   q E   x 1 m   v 0 2   x 1 2 +   x 2

Agora bastar achar uma expressão para substituir v o e E , podemos usar a definição de energia cinética para a velocidade e expressar o campo por meio da diferença de potencial:

K = 1 2   m   v 0 2

v 0 2 = 2 K m    

Agora o campo E :

E = V d

Substituindo os termos na equação temos:

∆ y =   q E   x 1 m   v 0 2   x 1 2 +   x 2

∆ y =   q V d   x 1 m   2 K m   x 1 2 +   x 2

∆ y =   q V x 1 2   d   K     x 1 2 +   x 2

∆ y =   1.602   x   10 - 19 C 25.0   V   ( 6.00 c m ) 2   ( 1.20 c m )   ( 2.80   k e V )     6.00   c m 2 +   30.0 c m

∆ y =   7.37   m m

FINALMENTE, alcançamos o santo graal, tudo feito, tudo pronto, fica bem, bons estudos e até a próxima!

Resposta

∆ y =   7.37   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elétron é lançado conforme mostrado na Fig. 26-41, com uma velocidade v 0 = 5,83 × 10 5m / s e a um ângulo θ = 39 , 0 ∘ ; E = 1870N / C (direcionada para cima), d = 1,97c m e L = 6,20c m . O elétro
Duas placas paralelas de cobre estão separadas por 5,00c m e têm um campo elétrico uniforme entre elas, conforme indicado na Fig. 26-40. Um elétron é largado da placa negativa no mesmo instante em que
Por que, simplesmente, não definimos a direção e o sentido do campo magnético B como sendo idênticos aos da força magnética que atua sobre uma carga em movimento?